|
Andrea Bellelli Department of Biochemical Sciences “A. Rossi Fanelli”, Sapienza University of Rome, Italy A lecture not yet given. ABSTRACT Ligand-linked association/dissociation phenomena occur when the aggregation state of am multi-subunit protein depends on the concentration of the protein ligand(s); this in turn requires that the ligand affinity of the protein differs in th edifferent aggregation states. Ligand-linked association/dissociation is common and very relevant in biology: e.g. it occurs in hemoglobin, hormone receptors, etc.; in the latter case the biological response may depend on the aggregation state of the receptor, rather than on the binding of the hormone, whose role is thus indirect. The quantitative treatment of ligand-linked association/dissociation is very complex, and in this lecture only the simplest case is analyzed, i.e. that of the symmetric homodimer in equilibrium with its constituent monomers. Selected references by the author Bellelli A and Carey J. (2018) Reversible Ligand Binding, Wiley. 1. LIGAND BINDING REACTIONS FOR A HOMODIMER IN EQUILIBRIUM WITH ITS MONOMERS The ligand binding reaction scheme for a homodimer that reversibly dissociates into its constituent monomers is as follows. 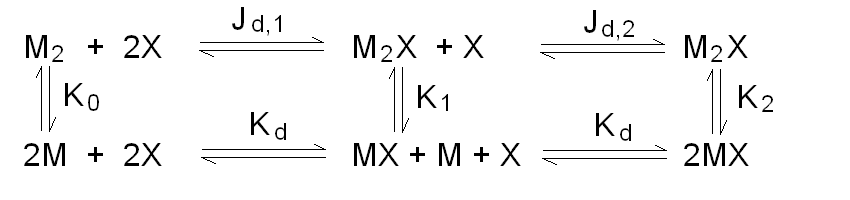 This reaction scheme includes six chemical species (M, MX, M2, M2X, M2X2, and X) whose chemical equilibrium is governed by six constants, only four of which are independent of each other. One is free to decide which constants are independent and I shall use the following: K0 = [M]2 / [M2] Kd = [M][X] / [MX] Jd,1 = [M2][X] / [M2X] Jd,2 = [M2X][X] / [M2X2] Moreover we remark that: Jd,1 Jd,2 = [M2][X]2 / [M2X2] The two remaining equilibrium constants are defined as follows: K1 = [M][MX] / [M2X] = K0 Jd,1 / Kd K2 = [MX]2 / [M2X2] = K0 Jd,1Jd,2 / Kd2 Moreover we can define the dissociation coefficient α as follows: α = [M] (1 + [X]/Kd) / Mtot where Mtot indicates the total concentration of the protein expressed in monomers. We can express the concentrations of all ligation intermediates as a function of those of the free monomer ([M]) and the free ligand ([X]): [MX] = [M] [X]/Kd [M2] = [M]2/K0 [M2X] = [M]2/K0 2[X]/Jd,1 (where the term 2 is the statistical coefficient to be applied to Jd,1) [M2X2] = [M]2/K0 [X]2/Jd,1Jd,2 The total protein concentration results: Mtot = [M] + [MX] + 2[M2] + 2[M2X] + 2 [M2X2] = = [M] (1 + [X]/Kd) + 2[M]2/K0 (1 + 2[X]/Jd,1 + [X]2/Jd,1Jd,2) (eqn. 1) The last equation allows one to solve [M] as a function of Mtot and [X]. Indeed we may rearrange it as follows: 2[M]2/K0 (1 + 2[X]/Jd,1 + [X]2/Jd,1Jd,2) + [M] (1 + [X]/Kd) - Mtot = 0 and solve: 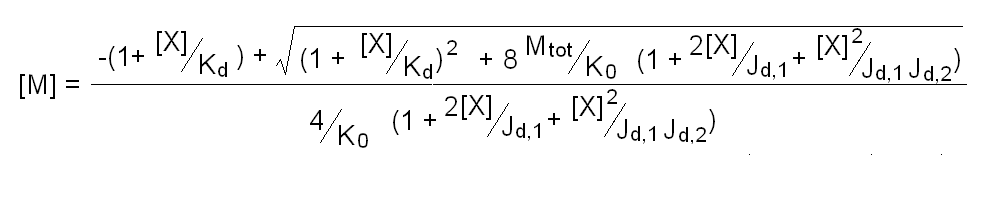 (eqn. 2) (eqn. 2)Thus, one can use the thermodynamic relationships given above to express the concentration of the free monomer in solution as a function of total protein concentration (Mtot) and free ligand concentration ([X]). This allows one to predict the concentrations of all chemical species in any type of ligand binding experiments, as I shall describe under section 3. 2. THE SPECIAL CASE OF LIGAND-INDEPENDENT DISSOCIATION Before describing the ligand binding isotherms of the homodimer in the presence of its monomers, I shall consider a special case in which the relationships given in section 1 undergo some simplification. Studying the simplifications and special cases is rewarding because we can easily predict their behaviour and conformity of the equations to the predictions is a check of the entire procedure. If the dimer is non-cooperative, and has the same ligand affinity as the monomer, one has the following condition: Kd = Jd,1 = Jd,2. This condition requires only one equilibrium dissociation constant (Kd), and entails that the dissociation of the dimer into monomers is ligand-independent, i.e.: K0 = K1 = K2. The fraction of monomers, in whatever state of ligation, does not depend on the ligand concentration, as one may verify from the following ralationship: 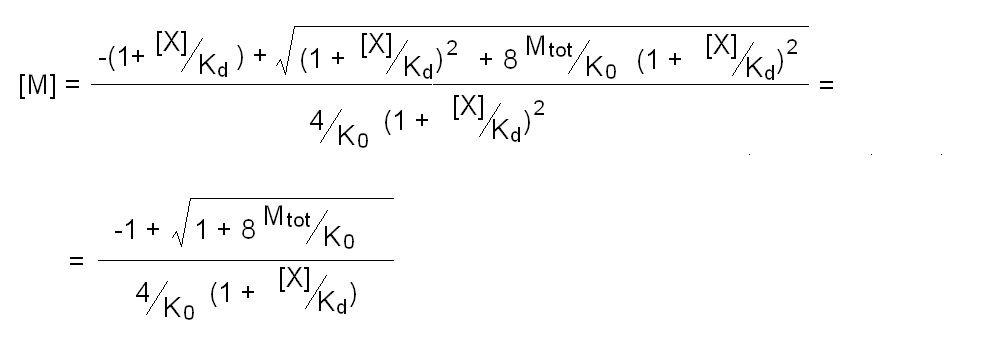 which demonstrates that the term [M](1 + [X]/Kd), representing the total concentration of the monomer in its liganded and unliganded state, is a function of Mtot but non of [X]. The above equation is fully equivalent to Ostwald law for the dimer-monomer equilibrium, as I demonstrate below. 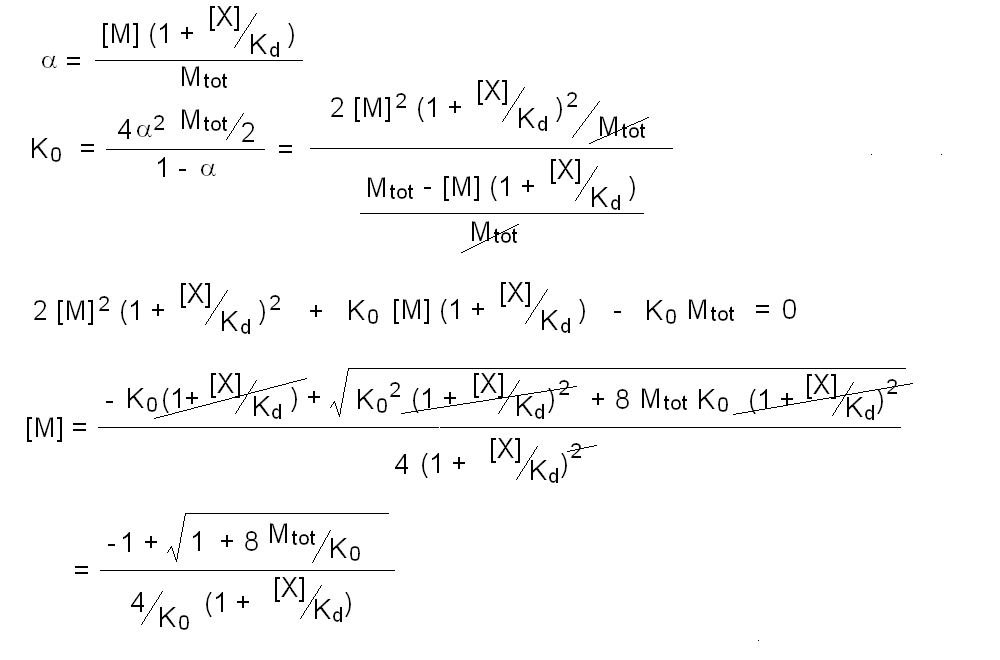 Thus, the analysis of ligand-independent dissociation demonstrates that the equations developed in section 1, under the special circumstance Kd = Jd,1 = Jd,2, reduce to an application of Ostwald law and gives us confidence on the correctness of the procedure. 3. THE BINDING POLYNOMIAL OF THE HOMODIMER IN EQUILIBRIUM WITH ITS MONOMERS I shall now turn to the most general case, described in section 1 and I shall develop its binding polynomial and fractional ligand saturation functions. Several interesting conditions may occur depending on the different possible combinations of the relative magnitude of the ligand dissociation constants. In the general case, the concentration of the unliganded monomer is defined by eqn. 2 and the binding polynomial by eqn. 1; the fractional ligand saturation and the degree of dissociation α are as follows. 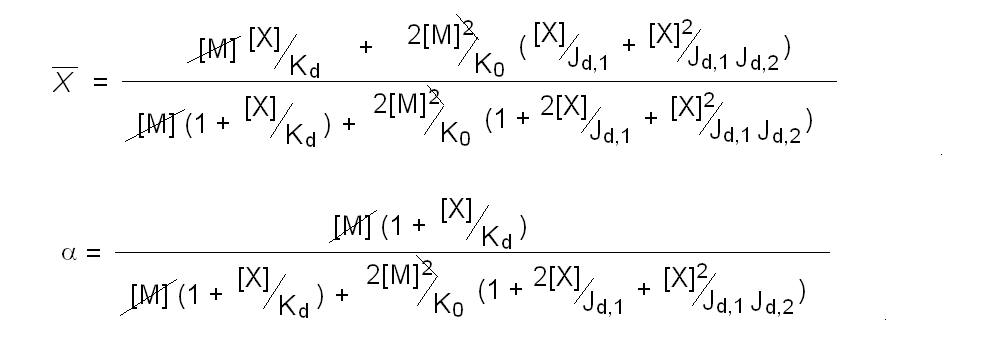 Depending on the values of the ligand dissociation constants one may have different practical cases, of which I shall analyze the most common and informative. 3a. The non-cooperative homodimer If the homodimer is non-cooperative, one needs not consider two ligand dissociation constants for the homodimer, i.e. Jd,1 = Jd,2. In this case only one dissociation constant is required for the homodimer (Jd), and the binding polynomial, monomer concentration, fractinal ligand saturation and degree of dissociation result as follows. 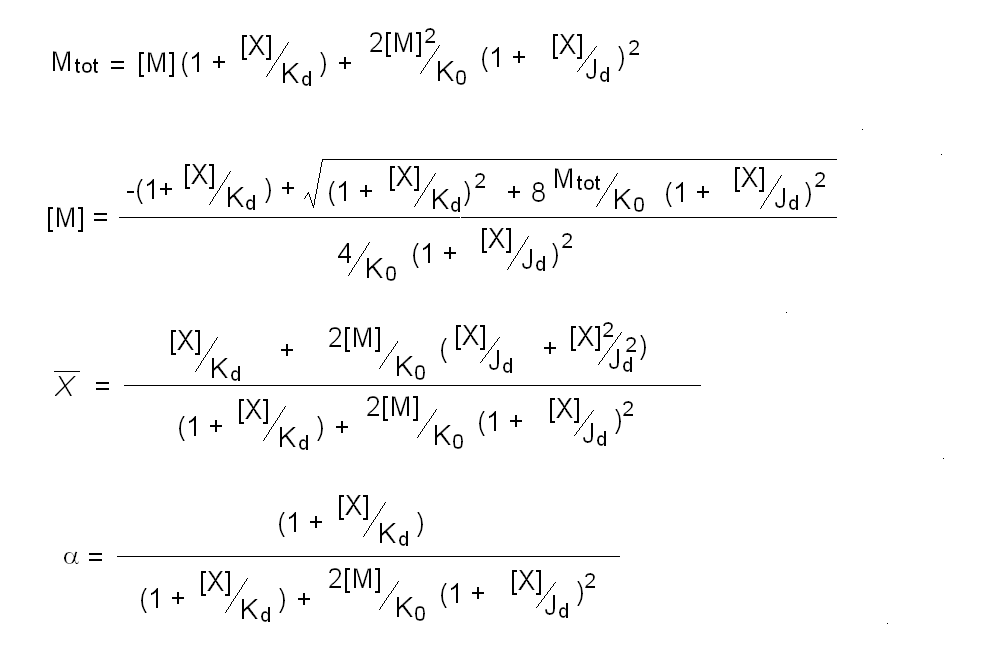 This case does not allow easy predictions because we still have three different dimer-monomer dissociation constants (K0, K1, and K2). However, this system presents an interesting characteristic: it exhibits cooperativity because of the selection by the ligand of the highest affinity state of the protein (either the monomer or the dimer), provided that the total protein concentration (Mtot) is such that α changes as a function of the free ligand concentration ([X]), as depicted in the figure below. 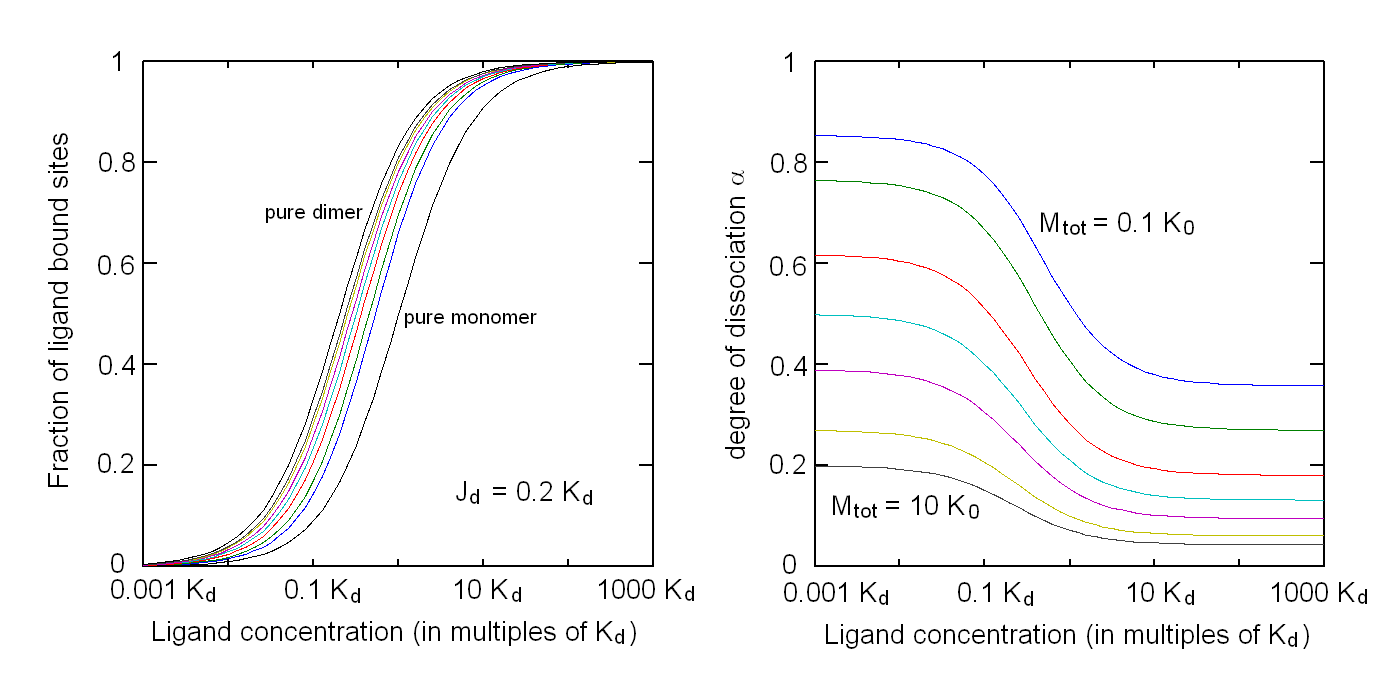 I remark that (i) ligand-linked dissociation causes the affinity for the ligand to depend on protein concentration (see left panel). (ii) Ligand-linked dissociation introduces cooperativity (i.e. a steeper ligand binding curve, see the left panel) because the ligand selects the higher affinity state, in the above example the dimer, and increases its population at the expenses of the lower affinity state (the monomer; see the right panel). (iii) In some biological phenomena, e.g. some hormone receptors, the physiological function of the effector is not mediated by the fractional saturation (left panel) but by the ligand-linked association of the protein (right panel). (iv) In this simulation, Jd is 5-fold lower than Kd, causing the dimer to monomer dissociation constant to decrease by 25-fold in the presence of saturating ligand concentrations (i.e. K2 = 0.04 K0); thus, a significant population of dimers forms even at the lowest total monomer concentration (Mtot = 0.1 K0 = 2.5 K2). The opposite occurs if Jd is higher than Kd (compare the right panels of Figs. 1 and 2). 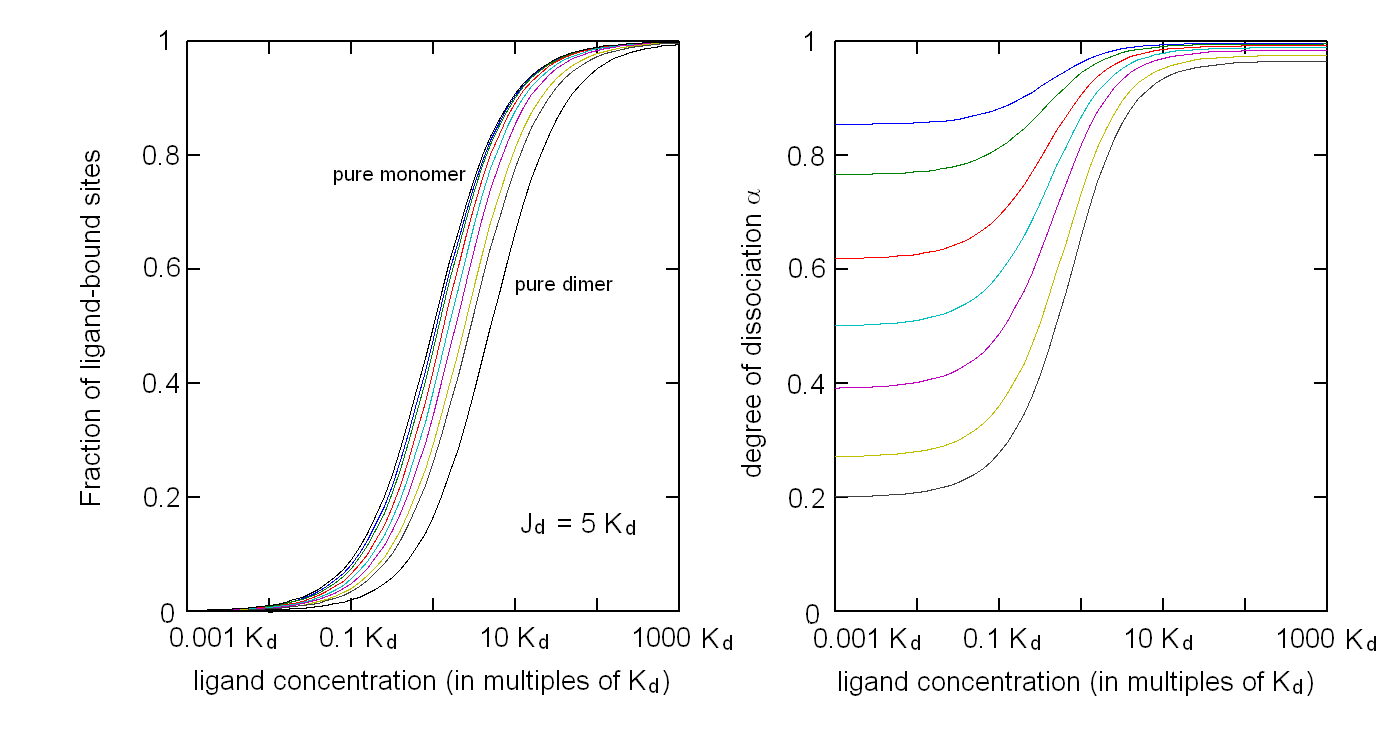 Home page |