PRIMA FACOLTA' DI MEDICINA E CHIRURGIA - CLM "B"
SAPIENZA UNIVERSITA' DI ROMA
Il programma del Corso Integrato di Chimica e Propedeutica Biochimica inizia con lo studio dell'atomo e copre per intero il programma di esame: non e' richiesta allo studente una conoscenza della Chimica di livello liceale, per una precisa scelta didattica. Infatti la disparita' dei programmi liceali non consente di dare per scontate neppure le conoscenze elementari della Chimica. Il programma pero' richiede allo studente il possesso di elementari nozioni di algebra e di matematica, che vengono di seguito elencate, insieme alle indicazioni necessarie ad un loro ripasso, che deve essere effettuato utilizzando i testi del Liceo.
Si chiama funzione una relazione algebrica tra due o piu' variabili tale che dato il valore di alcune sia possibile ricavare quello delle altre. Tipicamente una funzione avra' una o piu' variabili indipendenti, che il ricercatore puo' variare a suo piacimento e una o piu' variabili dipendenti il cui valore e' determinato dal valore assunto dalle variabili indipendenti.
Un esempio di funzione e' dato dall'equazione di stato dei gas perfetti, che stabilisce una relazione algebrica tra tre variabili indipendenti (quantita' di materia, espressa in moli e indicata con "n", temperatura assoluta, "T" e volume, "V"), una costante ("R") e una variabile dipendente (pressione, "P"):
P V = n R T
Lo studente deve essere in grado di ricavare la variabile dipendente (o qualunque altra variabile) dal valore delle altre, effettuando semplici trasformazioni algebriche; nel caso in esame:
P = n R T / V
Una funzione puo' essere rappresentata in un grafico formato da due (o tre) assi ortogonali su ciascuno dei quali viene riportato il valore di una variabile. In questa rappresentazione, ideata dal matematico francese Rene' Descartes (Cartesio) e denominata Cartesiana in suo onore, la funzione assume la forma di una linea retta o curva (o anche una superficie nel caso di tre assi) che unisce i punti le cui coordinate obbediscono alla relazione algebrica definita dalla funzione: ad esempio e' possibile riportare in grafico la dipendenza della pressione dalla temperatura o dal volume per il caso dell'equazione di stato dei gas considerato sopra:
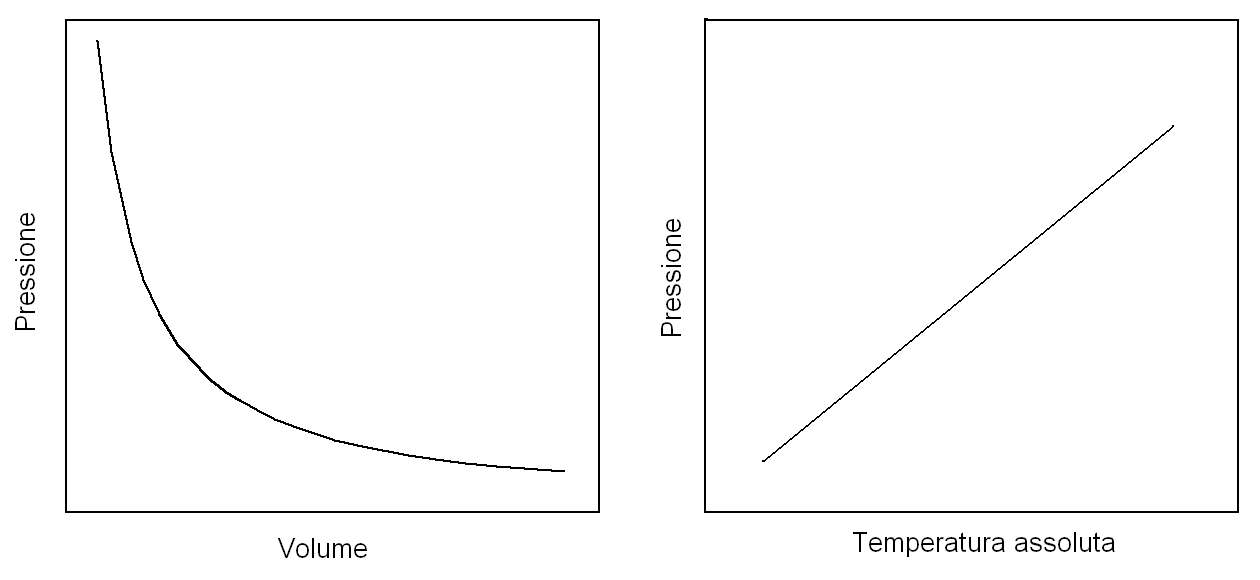
Figura 1: Le rappresentazioni dell'iperbole (a sin.) e della retta (a ds.), corrispondenti alle funzioni che correlano P con V e P con T.
.
Dato un numero non negativo, si chiama logaritmo (abbreviato log) l'esponente al quale deve essere elevata una base scelta in precedenza per ottenere il numero dato; ovvero:
logbase (n) = a
basea = n
In pratica si usano soltanto due basi per i logaritmi: 10 oppure il numero irrazionale e (approssimato a 2,7188). I logaritmi in base 10 si chiamano decimali, mentre i logaritmi in base e si chiamano naturali o neperiani. Ad esempio il pH e' il logaritmo decimale cambiato di segno della concentrazione dello ione idrogeno:
pH = - log (concentrazione ione idrogeno)
Se si conosce il logaritmo di una variabile e se ne vuole calcolare il valore occorre fare l'operazione inversa, che e' l'elevamento a potenza; ovvero per il pH, che e' un logaritmo decimale cambiato di segno:
(concentrazione ione idrogeno) = 10-pH
Poiche' i logaritmi sono esponenti, se una variabile viene riportata nella forma del suo logaritmo, tutte le funzioni alle quali essa partecipa cambiano forma: i prodotti diventano somme, i rapporti differenze, le potenze moltiplicazioni. Per convertire un numero nel suo logaritmo si utilizzano le tavole, il regolo calcolatore o la calcolatrice elettronica con la funzione log (per il logaritmo decimale) o ln (per il logaritmo naturale).
L'uso dei logaritmi introduce due nuove funzioni che possono essere rappresentate su un grafico cartesiano, chiamate la funzione logaritmica e la funzione esponenziale:
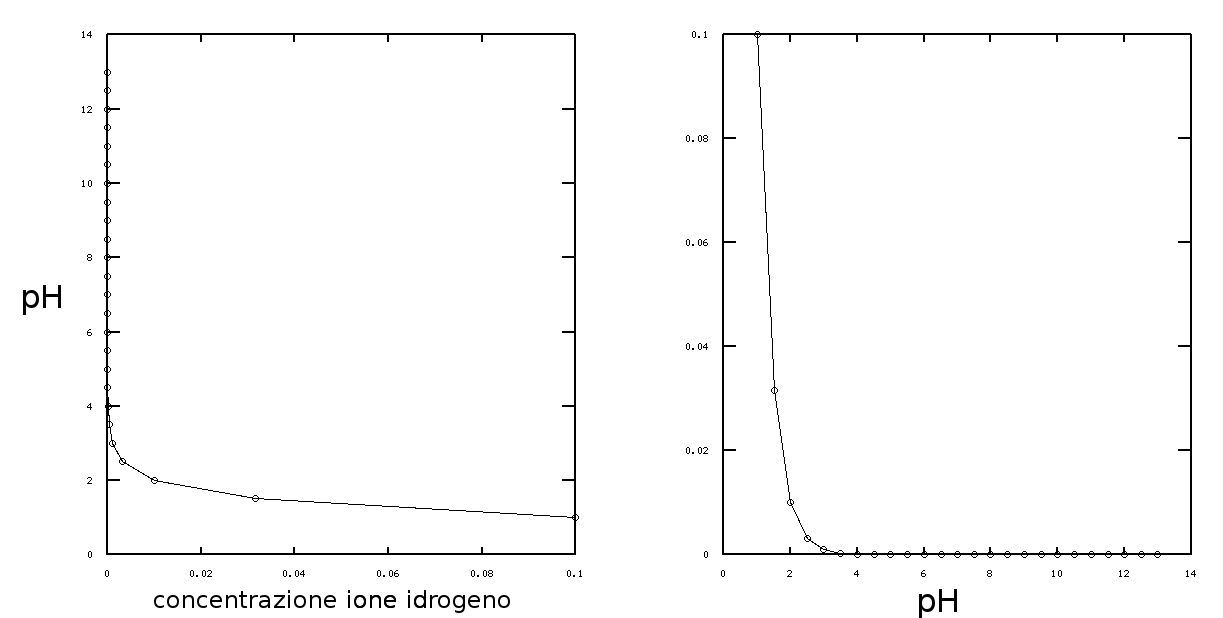
Figura 2: Le rappresentazioni delle funzioni logaritmica (a sin.) ed esponenziale (a ds.).
Le funzioni logaritmica ed esponenziale risultano pertanto molto utili quando e' necessario rappresentare nello stesso grafico, in forma ben visibile, numeri molto piccoli insieme a numeri molto grandi; in alcuni casi pero' comprimono i dati di interesse in curve molto ripide o molto piatte (come nella figura precedente).
Molti fenomeni naturali avvengono in modo apparentemente o intrinsecamente casuale. Casualita' non e' sinonimo di "privo di legge" o "non descritto da una funzione algebrica" o "caotico": un evento casuale e' governato dalle leggi della probabilita'. Ad esempio se si lancia un dado da gioco con le facce numerate da 1 a 6, ogni numero ha la stessa probabilita' di ogni altro: abbiamo 1 probabilita' su 6 di ottenere 1, 1 su 6 di ottenere 2, etc.
Per il teorema dei grandi numeri (o di Poisson) la probabilita' coincide con la frequenza dei risultati ottenuti in un grande numero di ripetizioni identiche dell'evento probabilistico: se tiriamo il dado 6 milioni di volte otterremo (circa) un milione di volte 1, (circa) un milione di volte 2, etc.
Si definisce probabilita' di un evento il rapporto tra il caso desiderato o considerato e il numero totale dei casi possibili.
La frequenza dei casi possibili ne rappresenta la distribuzione e puo' essere riportata su un grafico cartesiano, che abbia il caso considerato sull'ascissa e la sua probabilita' o frequenza sull'ordinata. Di solito la rappresentazione di una distribuzione avra' una forma a campana (gaussiana), nella quale i casi "intermedi" hanno frequenza maggiore dei casi "estremi".
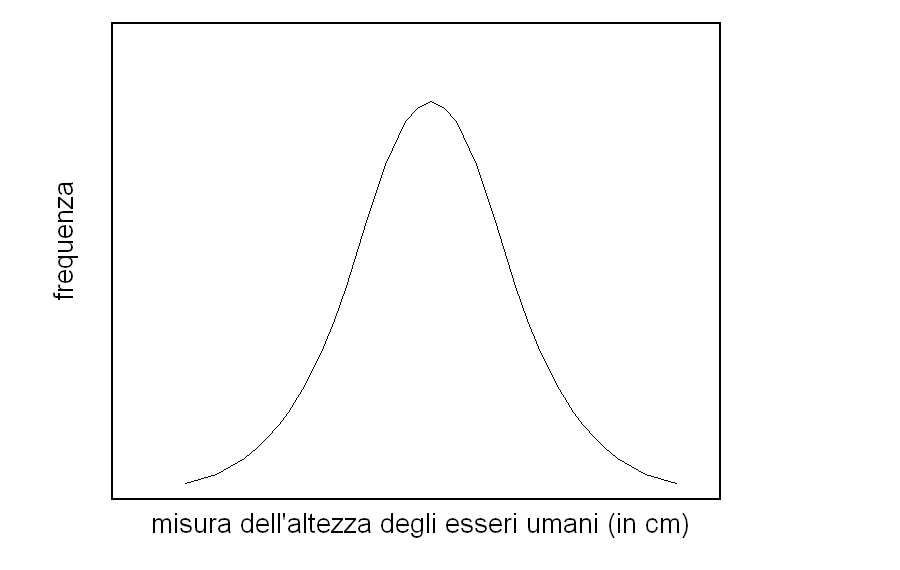
Figura 3: Distribuzione a campana dell'altezza degli esseri umani.
Le probabilita', essendo frazioni, si possono moltiplicare tra loro o si possono comporre in espressioni algebriche piu' complesse. Ad esempio se si tira il dado una volta, la probabilita' di ottenere 1 e' 1/6; se si tira il dado due volte, la probabilita' di ottenere due volte 1 e' pari al prodotto della probabilita' di ottenere 1 al primo tiro e di quella di ottenere 1 al secondo tiro; ovvero:
P (1) = 1/6
P (1;1) = 1/6 x 1/6 = 1/36
Torna a: didattica; pagina iniziale.