PRIMA FACOLTA' DI MEDICINA E CHIRURGIA - CLM "B"
SAPIENZA UNIVERSITA' DI ROMA
La cinetica chimica indaga la velocita' e il meccanismo delle reazioni chimiche.
Lo studio della cinetica chimica e' molto importante per la medicina: in primo luogo perche' le molecole del nostro organismo non si trovano nella loro condizione di equilibrio e la velocita' delle reazioni nelle quali sono coinvolteha importanza fondamentale per i fenomeni biologici; in secondo luogo perche' la decisione sul dosaggio e la via di somministrazione dei farmaci e' dettata in larga misura dalla velocita' con la quale essi sono assorbiti ed eliminati dal nostro organismo.
Il decadimento di un isotopo radioattivo e' un buon esempio di reazione semplice ed irreversibile, che coinvolge un solo atomo reagente e puo' essere schematizzata come segue:
La velocita' di reazione e' definita come il rapporto tra la variazione di concentrazione del reagente (presa con segno negativo) e l'intervallo di tempo considerato:
Poiche' ogni particella del reagente (A) ha la stessa probabilita' di ogni altra di trasformarsi nell'intervallo di tempo dt, e poiche' la concentrazione del prodotto (B) non ha effetto sulla reazione (irreversibile), si ha:
Questa equazione dimostra che la velocita' di reazione e' direttamente proporzionale a due termini: la concentrazione del reagente e un parametro (la costante cinetica "k") che indica la probabilita' che la reazione avvenga
La costante cinetica e' caratteristica di ogni reazione e dipende dalla temperatura.
L'equazione 3 e' una equazione differenziale che consente di calcolare la velocita' istantanea, oppure la variazione della concentrazione di reagente nell'intervallo di tempo dt:
Per rispondere alla domanda: "nota la k, quanto A si e' consumato al tempo t?", l'equazione deve essere integrata. Infatti, poiche' la concentrazione del reagente diminuisce nel tempo, proprio a causa della reazione cui esso va incontro, anche la velocita' di reazione diminuisce nel tempo; pertanto il reagente non scompare con velocita' costante ma con velocita' via via sempre minore. L'equazione che descrive questo fenomeno e':
dove [A]0 rappresenta la concentrazione iniziale del reagente e [A]t la sua concentrazione al tempo t, successivo all'inizio della reazione. La rappresentazione grafica di questa equazione e' una curva esponenziale che descrive la variazione della concentrazione del reagente A nel tempo:
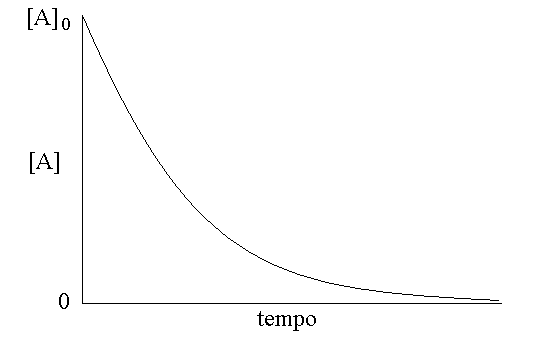
Figura 1: Decadimento esponenziale del reagente A nella reazione A --> B.
L'equazione 5 puo' essere linearizzata trasformandola in forma logaritmica:
Se si riporta in un grafico cartesiano il tempo (in ordinata) e il logaritmo della concentrazione di A (in ascissa) si ottiene una retta che ha come intercetta il logaritmo della concentrazione iniziale di A (ln[A]0) e come coefficiente angolare la kostante cinetica cambiata di segno (-k).
I passaggi essenziali della procedura di integrazione dell'eq.3 (non in programma) sono i seguenti:
Un parametro molto interessante dello sviluppo temporale di una reazione chimica e' il tempo di dimezzamento (t1/2), definito come il tempo necessario perche' la concentrazione del reagente si riduca alla meta' della concentrazione iniziale. Nel caso delle reazioni che seguono una cinetica esponenziale come quelle considerate finora il t1/2 e' indipendente dalla concentrazione iniziale del reagente e dipende unicamente dalla costante cinetica.
Considerando che quando t=t1/2 si ha [A]t1/2/[A]0=1/2, si puo' riarrangiare l'equazione 6 per ricavare:
I concetti di decadimento esponenziale e tempo di dimezzamento sono molto importanti per la medicina: infatti qualunque sostanza estranea introdotta nell'organismo (farmaci, veleni) ha una sua cinetica di eliminazione, spesso esponenziale, e i parametri k e t1/2 determinano quanto rapidamente l'organismo se ne libera (o quanto frequentemente si deve ripetere la somministrazione). Ad esempio la digossina, un farmaco attivo sul cuore, viene eliminata dall'organismo con una cinetica esponenziale ed un tempo di dimezzamento di circa 1 giorno: quindi il farmaco deve essere somministrato almeno una volta al giorno.
Un altro esempio di uso del tempo di dimezzamento rilevante per la medicina (e l'igiene) e' il seguente: calcolare dopo quanto tempo la concentrazione di un inquinante (ad es. un isotopo radioattivo) si riduce al di sotto dell'1% (o di qualuque altro valore di soglia) della sua concentrazione iniziale. Per rispondere a questa domanda consideriamo che dopo un tempo di dimezzamento la concentrazione del reagente e' il 50% di quella iniziale; dopo due tempi di dimezzamento e' il 25% (cioe' il 50% del 50%), e come formula generale si riduce secondo la legge 0,5n dopo n volte il tempo di dimezzamento. poiche' 0,57 = 0,0078 la risposta al problema e' che la concentrazione della sostanza si riduce a meno dell'1% del suo valore iniziale dopo circa 7 volte il tempo di dimezzamento.
Si definisce MOLECOLARITA' di una reazione chimica il numero di molecole che devono incontrarsi perche' la reazione possa avvenire; si definisce invece ORDINE di reazione il grado del monomio o del polinomio che ne esprime la legge cinetica. L'ordine di reazione non puo' essere dedotto dalla stechiometria e deve essere determinato sperimentalmente; pero' nei casi semplici (cioe' quelli in cui la reazione avviene in un unico atto di trasformazione e non in una serie di passaggi successivi) ordine e molecolarita' coincidono. Ad esempio, come abbiamo visto sopra, il decadimento radioattivo coinvolge un'unica specie chimica (un isotopo radioattiovo) ed e' quindi monomolecolare; nella sua legge cinetica (v = -d[A] / dt = k[A]) compare la sola concentrazione del reagente con esponente uguale ad uno quindi la reazione e' di primo ordine.
Un esempio di reazione bimolecolare importante nella medicina, che richiede l'incontro di due molecole di reagenti, e' la combinazione della mioglobina con l'ossigeno:
dove Mb rappresenta la mioglobina desossigenata, una piccola emoproteina presente nel tessuto muscolare, ed MbO2 la mioglobina ossigenata. Questa reazione e' di secondo ordine perche' segue la legge cinetica:
nella quale compare il prodotto tra due concentrazioni ([Mb] e [O2]) e quindi corrisponde ad un monomio di secondo grado.
In alcuni casi ordine e molecolarita' possono non coincidere e pertanto l'ordine di reazione deve sempre essere determinato sperimentalmente; in genere questo accade perche' la reazione considerata non e' semplice ed avviene in piu' eventi di trasformazione consecutivi.
Una reazione chimica che coinvolga piu' di due reagenti molto difficilmente avviene mediante l'urto simultaneo di tutte le molecole coinvolte: le probabilita' di un simile evento sono infatti molto basse. In genere due molecole si urtano e formano un intermedio a vita breve, che puo' dissociarsi restituendo i reagenti o andare incontro ad un ulteriore urto con la terza molecola per generare i prodotti. Ad esempio la reazione:
avviene grazie alla formazione dell'intermedio instabile N2O2 che puo' incontrare una molecola di ossigeno e trasformarsi nei prodotti, secondo il meccanismo di reazione seguente:
Una rappresentazione figurativa di questo meccanismo e' riportata nell'animazione qui sotto:

Figura 2: La reazione 2 NO + O2 <==> N2O2 + O2 <==> 2 NO2
In un caso come questo la trasformazione richiede tre molecole di reagenti (cioe' e' trimolecolare) ma avviene grazie a due reazioni elementari successive, ciascuna bimolecolare e di secondo ordine.
La reazione di combinazione della mioglobina con l'ossigeno, considerata sopra, e' reversibile e non va a completamento ma ad equilibrio. Dal punto di vista della cinetica questo si spiega con la coesistenza di due reazioni elementari, diretta ed inversa, del tutto indipendenti l'una dall'altra, descritte dalle equazioni:
Se noi mescoliamo una soluzione di mioglobina con una di ossigeno osserviamo inizialmente la sola combinazione tra i reagenti; man mano che il prodotto si forma comincia ad avvenire anche la reazione di dissociazione, la cui velocita' aumenta tanto piu' quanto piu' prodotto si forma. Per contro la velocita' di formazione del prodotto diminuisce man mano che i reagenti vengono consumati. L'equilibrio e' raggiunto quando le due velocita' di formazione e degradazione del prodotto si eguagliano: in queste condizioni la concentrazione dei reagenti e dei prodotti rimane costante nel tempo. Osserviamo che la condizione di equilibrio:
Tutte le reazioni chimiche, siano esse esotermiche o endotermiche, diventano piu' veloci quando si aumenta la temperatura, perche' i reagenti acquisiscono maggiore energia cinetica. Infatti si puo' immaginare che una reazione chimica tipica avvenga in due passaggi: nel primo si rompono (in genere a causa di un urto tra le molecole dei reagenti) i legami chimici caratteristici dei reagenti; nel secondo si formano i legami chimici caratteristici dei prodotti. Il primo passaggio richiede sempre energia perche' la rottura dei legami chimici e' sempre endoergonica, il secondo passaggio cede sempre energia perche' la formazione dei legami chimici e' sempre esoergonica. La reazione nel suo complesso e' esoergonica se l'energia assorbita nel primo passaggio e' minore di quella rilasciata nel secondo processo, endoergonica in caso contrario.
La relazione tra temperatura e costante cinetica di una reazione chimica e' data dalla legge di Arrhenius:
Nelle reazioni reversibili, un aumento di temperatura accelera sia la reazione cinetica diretta che quella inversa, ma non nella stesa misura (perche' in genere le due reazioni hanno energia di attivazione diversa). Come risultato anche la costante di equilibrio (che come ricordiamo e' pari al rapporto tra le costanti cinetiche delle reazioni diretta ed inversa) varia in modo non prefissato con la temperatura e puo', a seconda dei casi, aumentare o diminuire.
L'energia di attivazione puo' essere rappresentata in un grafico che riporti in ascissa la coordinata di reazione (qualunque parametro, spesso una distanza interatomica, utile per distinguere i reagenti dai prodotti) ed in ordinata l'energia corrispondente.
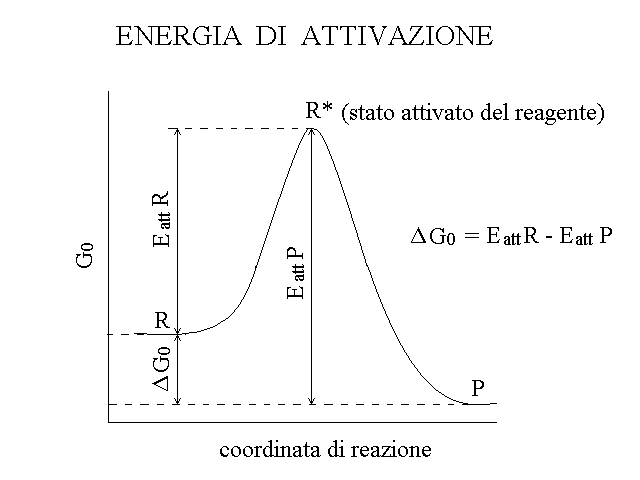
Figura 3: Energia di attivazione
Come si evince da questo grafico, l'energia di attivazione dei reagenti (EattR) e' diversa dall'energia di attivazione dei prodotti ((EattP), anche se entrambe riferiscono allo stesso stato attivato R*; inoltre la differenza tra le due energie di attivazione e' pari al delta G0 della reazione (e questa e' una conseguenza dell'eq. 19).
La catalisi e' il fenomeno per cui una sostanza che non partecipa alla stechiometria della reazione, causa un aumento della sua velocita'. Lo schema di una reazione catalizzata e' il seguente:
Come agisce un catalizzatore? L'eq. 21 ci dimostra che rispetto alla reazione non catalizzata (R <==> P), la reazione catalizzata e' piu' complessa e coinvolge almeno due reazioni distinte (R + cat. <==> R-cat. e R-cat. <==> P + cat.) e un intermedio instabile (R-cat.). Se il catalizzatore e' efficiente, l'energia di attivazione di entrambe le reazioni dello schema 21 e' piu' bassa di quella della reazione non catalizzata, come si vede nella figura seguente:
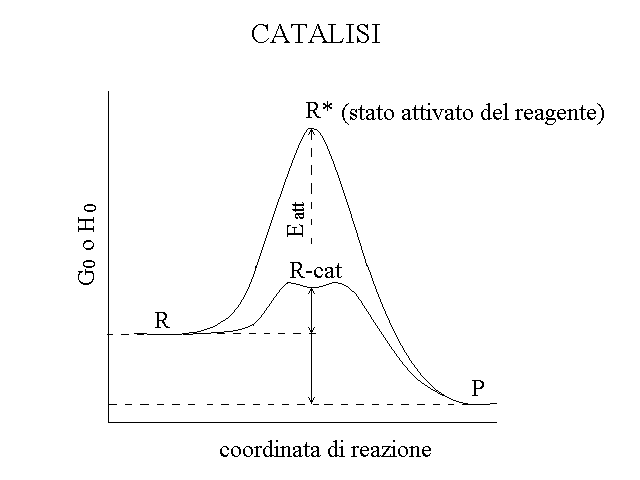
Figura 4: Effetto del catalizzatore sull'energia di attivazione
Gli enzimi sono proteine (composti che verranno studiati piu' avanti nel corso) che hanno attivita' di catalizzatori specifici: ogni enzima catalizza una ed una sola reazione biochimica (oltre naturalmente alla sua inversa). A volte l'unica reazione catalizzata dall'enzima puo' avvenire su due o piu' reagenti molto simili tra loro, altre volte su uno solo.
Il reagente delle reazioni catalizzate da enzimi viene chiamato il substrato di quell'enzima, e la relazione tra la velocita' della reazione e la concentrazione del substrato e' iperbolica anziche' lineare:
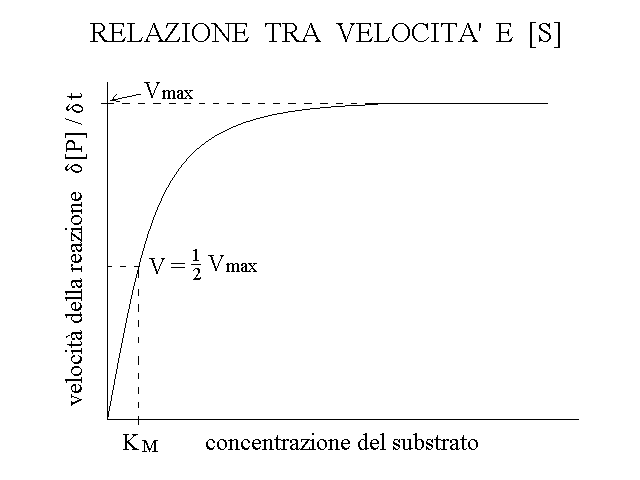
Figura 5: In presenza di un enzima la velocita' della conversione di S in P dipende dalla concentrazione di S secondo una funzione iperbolica
Per spiegare questo fenomeno, Michaelis e Menten ipotizzarono questo meccanismo di reazione (valido a tutt'oggi nelle sue linee essenziali):
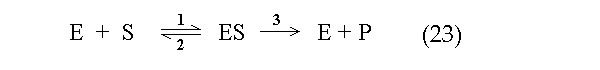
Il modello ipotizza che la conversione di S in P sia irreversibile. La reazione 1 e' bimolecolare e di secondo ordine e porta alla formazione del complesso di Michaelis (ES):
E + S --> ES d[ES] / dt = k1 [E][S] (24)
Le reazioni 2 e 3 sono entrambe monomolecolari e di primo ordine e degradano il complesso ES, la (2) verso la restituzione del substrato, la 3 verso la formazione e il rilascio del prodotto; entrambe restituiscono l'enzima libero (E):
ES --> E + S d[E] / dt = k2 [ES] (25)
ES --> E + P d[E] / dt = d[P] / dt = k3 [ES] (26)
La variazione della concentrazione del complesso ES nel modello di Michaelis risulta dalla somma algebrica delle velocita' delle reazioni di formazione (24, presa con segno positivo perche in questa ES viene prodotto) e di degradazione (25 e 26, prese con segno negativo, perche' in queste ES scompare):
d[ES] / dt = k1 [E][S] - [ES](k2 + k3) (27)
Lo scopo del modello e' quello di descrivere la cinetica di stato stazionario, nella quale il substrato viene consumato ed il prodotto viene formato con velocita' costante (ordine zero). Nella condizione di stato stazionario non si ha variazione della concentrazione di [ES] o di [E]: la velocita' con la quale ES si forma e' uguale a quella con la quale esso viene degradato (la condizione di stato stazionario non e' sempre realizzata: gli enzimi possono funzionare anche in condizioni di stato non stazionario; pero' queste condizioni non sono descritte dal modello di Michaelis). Quindi:
d[ES] / dt = 0 ; k1 [E][S] = [ES](k2 + k3) (28)
[E][S] / [ES] =(k2 + k3) / k1 (29)
Definiamo KM (costante di Michaelis) il rapporto =(k2 + k3) / k1:
KM =(k2 + k3) / k1 (30)
e consideriamo che la concentrazione totale dell'enzima e' costante e puo' essere definita come [Etot] = [E] + [ES]. Questo ci porta a riscrivere l'eq. 29 nella forma:
KM = ([Etot] - [ES]) [S] / [ES] (31)
che ci dimostra come la KM sia analoga ad una costante di equilibrio per la reazione di dissociazione del complesso ES. Ripetendo un ragionamento gia' condotto nello studio dell'equilibrio chimico, possiamo scrivere:
KM [ES] = [Etot][S] - [ES][S] (32)
[ES] (KM + [S]) = [Etot][S] (33)
[ES] / [Etot] = [S] / (KM + [S]) (34)
L'ultima equazione descrive la frazione di enzima presente nella forma del complesso ES in funzione della KM e della concentrazione del substrato e la sua rappresentazione grafica e' una iperbole che passa per l'origine degli assi (quando [S] = 0 si ha anche [ES] = 0)e presenta un asintoto superiore uguale ad 1 (quando [S]>>>[KM la somma [KM + [S] approssima [S] e quindi il rapporto [ES] / [Etot] approssima l'unita').
La velocita' della reazione catalizzata dall'enzima corrisponde alla velocita' di formazione del prodotto (eq. 26) e puo' essere riscritta come:
d[P] / d[t] = [ES]k3 = [Etot]k3 [S] / (KM + [S]) (35)
Quest'ultima equazione si chiama equazione di Michaelis e Menten e corrisponde molto bene alla figura 5. Quando la concentrazione del substrato e' molto maggiore della KM, quasi tutto l'enzima e' presente nella forma del compelsso ES, e la velocita' della reazione approssima un asintoto, che e' la sua velocita' massima:
Vmax = [Etot]k3 (36)
Dall'eq. 36 si puo' ricavare il temine k3 che risulta uguale al rapporto Vmax / [Etot]; in meccanismi enzimatici piu' complessi di quello considerato da Michaelis lo stesso rapporto corrispondera' ad una funzione piu' complessa delle costanti cinetiche e sara' chiamato kcat o numero di turnover dell'enzima. In ogni caso, a prescindere dalla complessita' del modello la kcat rappresenta il massimo numero di molecole di substrato che una molecola di enzima puo' convertire nell'unita' di tempo considerata (in genere 1 sec.).
1) l'enzima accelera una reazione chimica che altrimenti, alla temperatura dell'organismo, avverrebbe su scale di tempo incompatibili con quelle richieste dai processi vitali.
2) L'enzima e' specifico e accelera una sola reazione (con la sua inversa) su un solo substrato o su pochi substrati tra loro molto simili. Questo significa che producendo soltanto gli enzimi necessari in quel momento, la cellula puo' selezionare solo alcune tra le molte reazioni chimiche che potrebbero avvenire al suo interno. La specificita' dell'enzima per il suo substrato e' stata paragonata a quella della serratura per la sua chiave.
3) L'enzima puo' accoppiare tra loro due reazioni chimiche con delta G opposto e far quindi avvenire anche reazioni che sarebbero altrimenti sfavorevoli dal punto di vista termodinamico (pero' con consumo di energia, in genere sotto forma di ATP o NADH). Una rappresentazione della termodinamica di un caso di questo genere e' riportata nella figura 6:
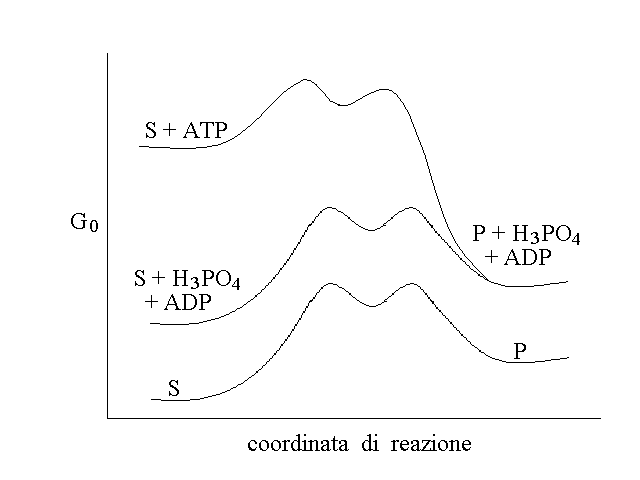
Figura 6: La reazione S --> P ha delta G > 0 ed e' quindi termodinamicamente sfavorevole; un enzima che la catalizzasse trasformerebbe P in S anziche' viceversa. Se la stessa reazione avviene in presenza di ADP e fosfato il delta G non cambia (ADP e fosfato non partecipano alla reazione e sono soltanto aggiunti al sistema). Un enzima puo' accoppiare alla conversione di S in P la reazione di idrolisi dell'ATP (ATP + H2O --> ADP + H3PO4) che ha delta G negativo; in questo caso il delta G complessivo e' la somma algebrica di quello delle due reazioni separate. Spesso questo avviene grazie al trasferimento di una molecola di acido fosforico dall'ATP al substrato (S + ATP + E --> ES-O-P(O3H2 + ADP --> E + P + ADP + H3PO4).
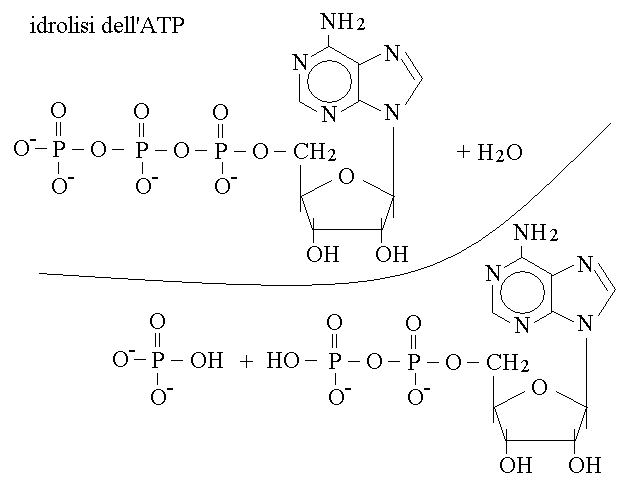
Figura 7: Formule dell'ATP (sopra) e dell'ADP (sotto) e loro possibile interconversione mediante idrolisi
I meccanismi molecolari della catalisi enzimatica non possono essere definiti in modo generale: ogni enzima ne adotta uno proprio. Si possono pero' fare delle considerazioni generali: infatti l'enzima e' una molecola molto grande, in grado di "contenere" il substrato ( parte di esso) e di stabilire con lui una rete estesa di legami chimici, in genere deboli, ma in alcuni casi anche covalenti. La parte della molecola dell'enzima che interagisce con il substrato ha in genere la forma di una cavita' e viene chiamata il sito attivo o il sito catalitico. I legami che si formano tra l'enzima e il substrato forzano una distorsione di quest'ultimo, che indebolisce il legame che deve essere rotto nella reazione catalizzata. Ad esempio, se l'enzima deve rompere un legame che ha una energia di 50 kcal/mole e stabilisce con il substrato sei interazioni deboli, ciascuna con energia di 5 kcal/mole, queste possono distorcere e indebolire il legame covalente fino ad abbassarne l'energia a 50 - (6x5) = 20 kcal/mole. Nei casi piu' semplici quindi il sito attivo dell'enzima non ha forma esattamente complementare a quella del substrato, ma ha forma complementare ad una molecola di substrato leggermente distorta, che assomiglia allo stato attivato della reazione S --> P.
INIBIZIONE ENZIMATICA. La cellula puo' produrre (o talvolta assorbire dall'esterno) sostanze che si combinano con gli enzimi e ne impediscono il funzionamento: gli inibitori enzimatici. Gli inibitori sono specifici per ogni enzima (o quasi) e possono agire con almeno tre diversi meccanismi: competitivo, non competitivo e allosterico. Esistono alcune varianti di questi meccanismi che rendono il quadro piu' complesso. Saranno esaminati in questo corso soltanto i due casi dell'inibizione competitiva e dell'inibizione non competitiva.
INIBIZIONE COMPETITIVA. Un inibitore competitivo si combina con il sito attivo dell'enzima ed impedisce il legame del substrato. Lo schema di reazione e' il seguente:
EI + S <==> E + I + S <==> ES + I --> E + I + P
In questo schema esistono tre possibili forme dell'enzima: E, ES ed EI ma non c'e' il complesso a tre EIS. La frazione di enzima presente nella forma di complesso EI dipende dalla concentrazione e dalla costante di equilibrio dell'inibitore (per convenzione si usa la costante di dissociazione del complesso EI). Se si prende come specie di riferimento l'enzima libero E, si puo' calcolare quante moli di ES e di EI sono in equilibrio con ogni mole di E:
[ES] = [E] [S] / KM
[EI] = [E] [I] / KI
[Etot] = [E] + [EI] + [ES] = [E] (1 + [S] / KM + [I] / KI)
L'ultima equazione ci chiarisce che aumentando la concentrazione del substrato e' possibile far diminuire a piacere quelle di E ed EI in favore di quella di ES: quindi nell'inibizione competitiva l'aumento della concentrazione del substrato spiazza l'inibitore e ripristina la velocita' massima.
INIBIZIONE NON COMPETITIVA. L'inibitore non competitivo si lega all'enzima in una posizione diversa dal sito catalitico e pertanto non inibisce la combinazione del substrato; le specie possibili sono E, ES, EI ed EIS. L'unica specie cataliticamente attiva e' ES, mentre le altre non hanno la capacita' di formare il prodotto (ed in particolare e' inattivo il complesso EIS). Nel caso tipico di questa inibizione, il legame con l'inibitore non altera l'affinita' dell'enzima per il substrato e pertanto il substrato si lega altrettanto bene ad E e ad EI. Di conseguenza un aumento della concentrazione del substrato non rimuove l'inibizione non competitiva e aumenta soltanto la popolazione della specie inattiva EIS.
Torna a: didattica; Medicine non Scientifiche; Biblioteca Digitale.