| Course of LABORATORY MEDICINE On the molecular mechanism of inherited enzymopathies Genetic defects that are inherited as Mendelian traits are due to single genes, and may be dominant or recessive. Sex-linked single gene enzymatic defects are located on the X chromosome, and, though non-Mendelian, share a similar biochemical mechanism. Diseases due to single gene inheritable enzymopathies may occur because of different biochemical mechanisms, of which we shall examine in this lecture only the most common. As a general rule the affected gene is not expressed, or, if expressed yields a non-functional or unstable enzyme variant. As a consequence the heterozygous patient has in his/her cells a reduced amount of the enzyme (produced by the normal gene) and the homozygous patient virtually lacks the enzyme altogether. We consider the two conditions seprately, under the assumption that the catalytic activity of affected enzyme can be described by the model of Michaelis and Menten and that the concentration of its substrate is produced by the metabolism at a constant rate. The heterozygous patient has half the normal enzyme concentration; as a consequence he processes the substrate at a rate that is half the normal rate. This condition causes the substrate to accumulate and its concentration in the body fluids to increase. However the substrate concentrations are usually close to the KM of the enzymes responsible for their metabolism. This occurs because this condition offers selective advantage, as increases or decreases of the substrate concentration are met by increases or decreases of the rate of consumption. Indeed accumulation of the substrate of the affected enzyme raises its concentration and allows the available enzyme to work more efficiently, as demonstrated by the following graph. 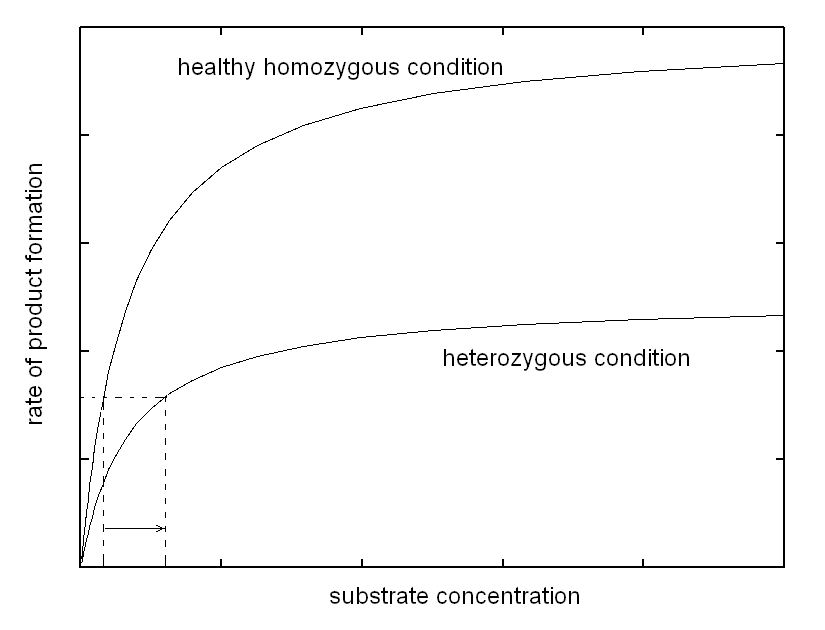
Thus, the enzyme, though present at lower than normal concentration, is able to process the substrate produced at a constant rate and to maintain the body homeostasis, at the expense of a more or less significant increase of substrate concentration. In other words, in the heterozygous patient increased concentration of a specific metabolyte, the substrate of the affected enzyme, partially compensates for the defect in enzyme concentration, via an increased catalytic efficiency of the available enzyme. Is the compensation effective, i.e. does it prevent the disease? The answer to this question defines the type of inherited disease: (i) if the substrate is toxic and damages some tissue (e.g. the brain of the affected infant) its accumulation may produce disease. In this case the defect is inherited as a dominant trait. (ii) If the substrate is non-toxic, the heterozygous condition is healthy and the defect is defined a recessive trait. (iii) Intermediate cases may occur defined as incomplete penetrance traits, in which the heterozygous patient suffers of a mild form of disease. The biochemical mechanisms underlying these cases are variable; e.g. if alternative pathways of disposal of the substrate are available, accumulation is prevented or reduced, but this works against the biochemical compensation described above and may produce shortage of the reaction product. The homozygous patient has a very severely reduced concentration of the affected enzyme or lacks it altogether. As a consequence, no increase in the concentration of the substrate can exert a compensatory effect. In this condition (i) the substrate accumulates to high levels; and (ii) there is shortage of the product (that usually is not present or not significant in the heterozyogous state). Polygenic (non-mendelian) hereditary diseases are frequent, either as diseases tout court or as conditions that predispose to or favor common diseases. The molecular mechanisms at the basis of polygenic diseases may be variable and are not always completely understood, thus a theoretical exercise that illustrates a plausible biochemical mechanism seems worthwhile, at least from a pedagogical viewpoint. In this exercise, we assume a very simple metabolic pathway, constituted by two reactions catalyzed by two enzymes. The reaction scheme is as follows: Metabolyte A is assumed to be produced at a constant rate, thus its concentration in the blood or tissues is constant. Metabolyte B is produced by enzyme E1 acting on substrate A. Metabolyte B is degraded by enzyme E2 that converts it to terminal metabolyte C which is excreted in the urine. We assume that both E1 and E2 obey a simple Michaelis-Menten catalytic mechanism. Our theoretical model assumes that metabolyte B is potentially toxic and its accumulation may cause disease. Examples of toxic metabolytes abound: e.g. this condition applies to acetaldehyde, the metabolyte of ethanol produced by alcol dehydrogenase and oxidized by the liver microsomial fraction; or to phenylpiruvic acid, produced by the osidative deamination of pheylalanine. Under steady state conditions, metabolyte B is produced and degraded at a constant rate and attains a constant concentration in the body fluids and tissues; we can easily calculate its concentration as follows: (i) the net rate of formation of B is obtained by subtracting the rate of degradation from the rate of production: d[B]/dt = [A]Vmax1/([A]+KM,1 - [B]Vmax2/([B]+KM,2 (eqn. 1) where Vmax1 and KM,1 are the steady state parameters of E1 and Vmax2 and KM,2 those of E2. (ii) If we assume that A is produced at a regulated rate and that its concentration is the same in all individuals (a considerable simplification of our model), we can easily solve the above equation under the steady-state assumption (d[B]/dt = 0) and we obtain: [B] = [A]Vmax1KM,2 / (Vmax2([A]+KM,1)-[A]Vmax1) We now suppose that the population contains two allelic variants of the genes encoding for E1 and E2. We name the respective genes and gene products E1 and e1, E2 and e2. All enzyme variants are perfectly functional and none of them by itself is associated to disease: thus the variants distribute in the population according to the Hardy-Weinberg law. In both cases the steady-state parameters of the two variants of the same enzyme differ only slightly; in the present simulation by only 10%. 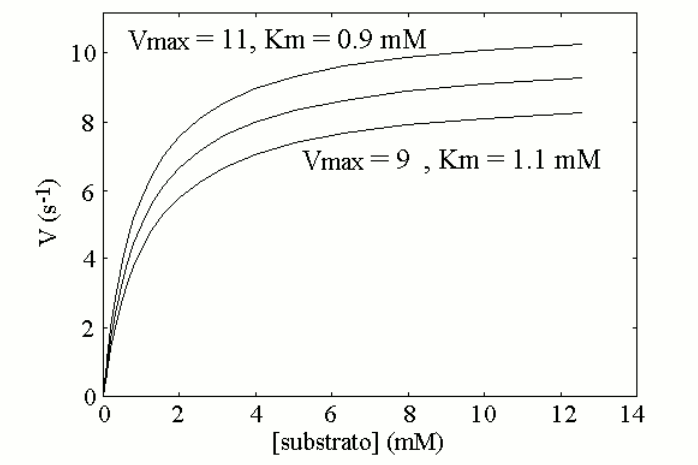
We now assign the gene frequencies of the two variants as follows: E1=40% (with e1=60%) and E260% (with e2=40%), and we simulate the distribution of the genotypes in the population assuming it to be purely statistic (i.e., Hardy-Weinberg). We obtain the following table: 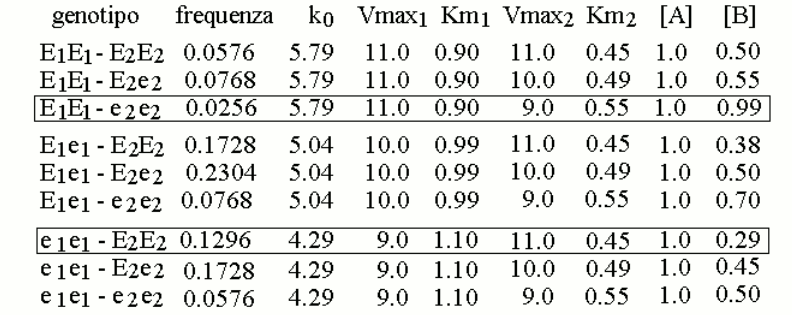
We further assume that a reasonable approximation of the steady state parameters of mixtures of the two variants E1 and e1 (or E2 and e2), present in heterozygous individuals, is provided by the weighted average of the Vmax and KM values of the enzyme variants, as reported in the table. This allows us to calculate the concentration of metabolyte B in the body fluids of individuals of different genotype/phenotype (also in the table). We can now graph the distribution of the concentration of metabolyte B in the body fluids of the members of the population: 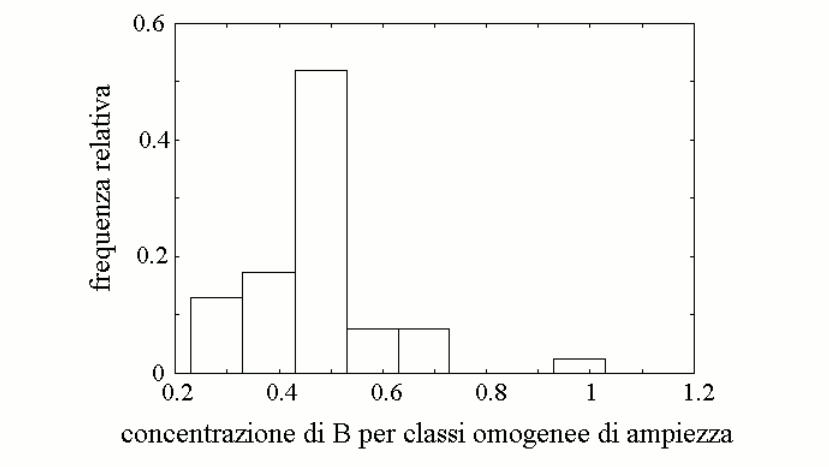
The graph is a skewed (asymmetric) Gaussian curve, and we remark that the frequency of the high-B subgroup does not correlate with the frequency of any specific gene variant. Indeed the high-B subgroup correspond to a very specific genotype, that of individuals who are homozygous for the high-efficiency variant of enzyme 1 (E1) and again homozygous for the low-efficiency variant of enzyme 2 (e2). 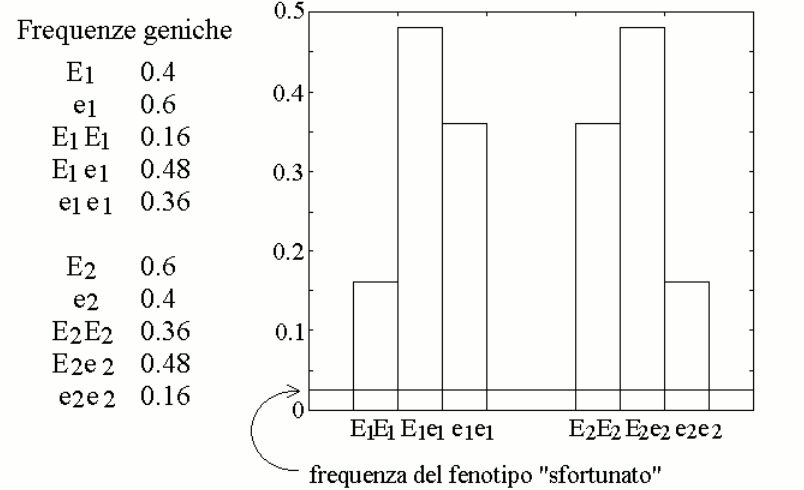
From a qualitative viewpoint, the result obtained with this simulation is expected and unsurprising: metabolyte B accumulates in those individuals who produce it rapidly and dispose of it slowly. What is surprising is that so small a change in the steady-state parameters of the two enzyme variants (10%, as in the figure above) cause such large a change in the concentration of the toxic metabolyte B (three-times higher than the average value for the population). How significant is a three-times larger concentration of a metabolyte? In many cases very significant: e.g., fasting glycemia in healthy humans ranges between 70 and 110 mg/dL and a three-fold increase to 300 mg/dL would be considered very significant. Thus, an unfortunate combination of otherwise "normal" allelic variants of enzymes of the same pathway may yield a (rare) phenotype prone to disease. Since the combination is rare, it is difficult to attribute to a specific gene: indeed in our model population there is plentiful of individuals homozygous for either E1 or e2 who have normal values of the toxic metabolyte B. Home of this course |