Andrea Bellelli
CHAPTER 1: MONOMERIC PROTEINS
1.1: MASS LAW
Ligand binding is the physiological function of many proteins: respiratory proteins bind oxygen; enzymes bind substrates and inhibitors; receptors bind effectors; and so on. From the view point of physical chemistry proteins are very complex molecules and their equilibria with ligands may be correspondingly complex, even though they may seem simple and straightforward. In what follows I shall try to address the most relevant issues from a theorethical standpoint.
The mass law applied to a monomeric protein (P) that combines reversibly with a single ligand (X) yields the following equations:
P + X <==> PX (1)
K = [PX] / [P][X] (2)
In many cases the inverse (dissociation) reaction is considered, to obtain Kd = [P][X] / [PX], e.g. when dealing with the P50 of respiratory proteins or with the KM of enzymes. The two formulations of combination and dissociation reactions are equivalent to each other and may be easily interconverted. In what follows I shall use mostly the former for the sake of consistency, except when the use sanctioned the latter, in which case I shall consider them both.
Two important functions can be derived from eq.2 i.e. the binding polynomial and the fractional ligand saturation (Y). The binding polynomial represents the total protein concentration as the sum of each chemical species of the protein present in solution, referred to a "reference" one. It is usual to take as the reference species the unliganded protein:
[P] = reference
[PX] = [P] [X]K
[P]total = [P] (1 + [X]K) (3)
The fractional saturation is the ratio between the liganded binding sites and the total number of binding sites (derived from the binding polynomial)
Y = [PX] / ([P] + [PX]) = [X]K / (1 + [X]K) (4)
Eq.4 demonstrates that Y is a hyperbolic function of the free ligand concentration [X], as is shown in Fig. 1.1.1A, which represents the fractional saturation of a monomeric protein with K = 104 M-1. An important and non-distorting representation of the same data set is that of Y versus log ([X]), which has the symmetric sigmoidal shape shown in Fig. 1.1.1B due to the fact that log ([X]) is proportional to the free energy of the ligand in solution (at least when [X] is low).
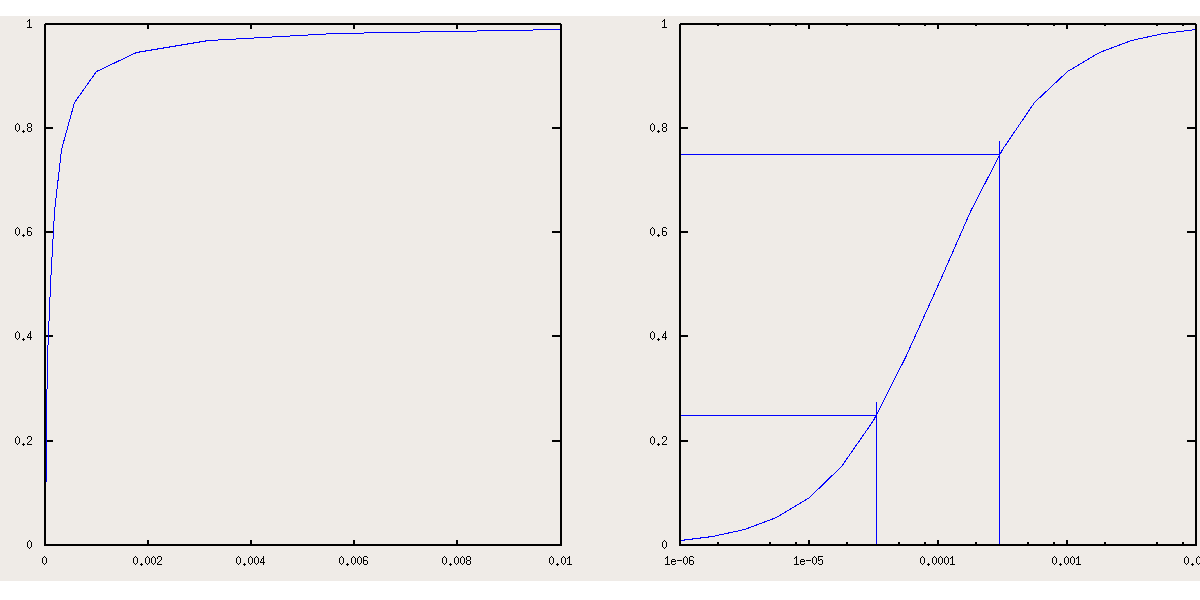
A relevant information is the free ligand concentration (X50) required to achieve half saturation (Y = 0.5); this corresponds to:
X50 = 1 / K
We remark that the combination equilibrium constant K has the units of M-1 (see eq.2); by contrast the dissociation equilibrium constant Kd = 1 / K has the units of a molarity and directly equals the X50 (this is one of the reasons why it is preferred by some authors).
From eq.2 the ligand concentrations corresponding to any value of Y can be derived, and it is interesting to explore couples of values that are symmetric with respect to 0.5: the formula to calculate these values is X0.5+N = 1/K (0.5 + N) / (0.5 - N) , with N positive or negative. Notice that this formula imposes symmetry of the Y vs. log[X] curve by 180o rotation arount the point of coordinates (1/K,0.5). We can ask which interval of ligand concentration is required to raise the fractional saturation from 0.25 to 0.75, and we obtain: X25 = 1 / 3 K; X75 = 3 / K (see Fig. 1.1.1B). This exercise demonstrates that a 9-fold increase of the free ligand concentration is required to increase the fractional saturation from 0.25 to 0.75. It is possible that an experimentally determined ligand equilibrium isotherm appears significantly steeper, or, vice versa, significantly less steep. We shall consider these case later on.
1.2: REPLACEMENT REACTIONS - COMPETITIVE LIGANDS
A replacement reaction occurs when two different ligands capable of binding to the same site in the protein are present. This is the case of enzyme inhibitors capable of competing with the substrate or of CO and O2 in respiratory hemoproteins. The reaction is as follows:
The system can be treated as a double equilibrium:
[P] = reference species
[PX] = [P] [X]KX
[PW] = [P] [W]KW
[P]total = [P] (1 + [X]KX + [W]KW)
YX = [X]KX / (1 + [X]KX + [W]KW)
However, this "complete" approach (which requires the determination of two equilibrium constants) is rarely necessary: as a general rule the concentration of the unliganded protein [P] is negligible, unless the concentrations of both ligands are very small. Thus the system can be simplified to:
KP = ([PX] [W]) / ([PW] [X])
[PW] = reference species
[PX] = [PW] Kp [X] / [W]
YX = ([Kp [X]/[W]) / (1 + Kp [X]/[W])
where Kp, the partition constant, is the ratio between the affinity constants of the two ligands X and W:
KP = ([PX] [W]) / ([PW] [X]) = ([PX] [W] [P]) / ([PW] [X] [P]) = KX / KW
If the experiment is carried out at constant concentration of one ligand, e.g. W (high enough to make negligible the amount of ligand that is bound to or dissociated from its complex with the protein), and varying only the concentration of the other, a simple hyperbolic function of Y (i.e. [PX]/([PX]+[PW]) versus [X] is obtained, whose apparent equilibrium constant and X50 are:
Kapp = KP / [W]
X50, app = [W] / KP
Replacement reactions are usefully exploited when the affinity of the protein for its ligand X is so high to hamper the determination of X50: indeed [W] can be increased almost at will (provided that it is soluble enough) thus causing X50, app to raise correspondingly.
Fig.121 reports the fractional saturation with ligand X as a function of the lograithm of [X] for a protein which has an affinity constant for X of 106 M-1 in the absence of the competing ligand W (leftmost curve) and in the presence of 1 and 10 mM W. In this example the affinity for W is KW = 104 M-1, thus the partition constant results KP = KX / KW = 100 and the apparent affinity constants for X in the presence of the two concentrations of W result 105 M-1 (at [W] = 10-3 M), and 104 M-1 (at [W] = 10-3 M).
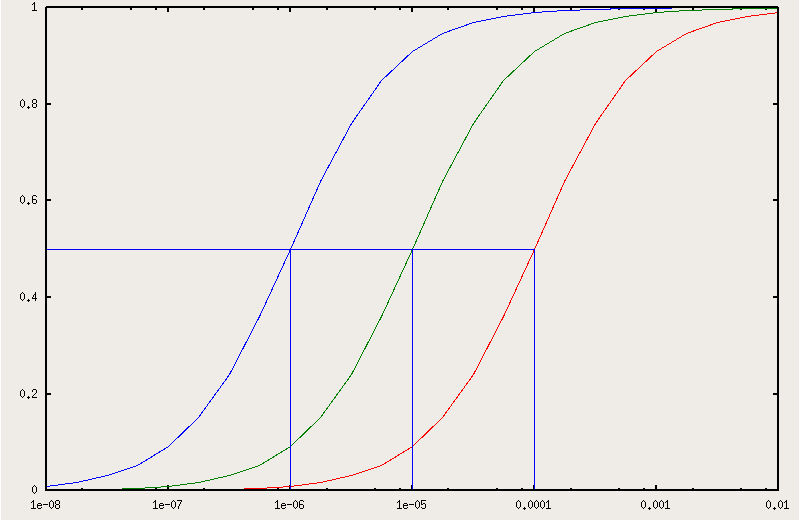
The right shift of the X binding curves in the presence of the competing ligand W is self evident and is most welcome when the intrinsic affinity is high (more on this point in chapter 2).
1.3: NON COMPETITIVE BINDING OF TWO LIGANDS - LINKED FUNCTIONS
This case is frequent in biology. It occurs when a monomeric protein has two different binding sites for two ligands that combine independently of each other. The resulting reaction scheme is as follows:
| KX | |||||
| P + X + W | <==> | PX + W | |||
| KW | | | | | XKW | ||
| WP + X | <==> | WPX | |||
| WKX |
The reaction scheme is a thermodynamic square and is effectively described by three independent equilibrium constants, the fourth being unequivocally determined by the other three. The demonstration is as follows:
KX = [PX] / [P][X]
KW = [WP] / [P][W]
XKW = [WPX] / [PX][W]
WKX = [WPX] / [WP][X] = KX XKW / KW
We remark that if XKW > KW, i.e. if binding of X increases the affinity for W, then WKX > KX, i.e. binding of W must increase the affinity for X, and vice versa.
We can take the concentration of one species of the protein and refer all the other to this, as a function of the affinity and concentration of the ligands. Using the concentration of unliganded protein as a reference, as usual, we obtain:
[P] = reference concentration
[PX] = [P] [X]/KX
[WP] = [P] [W]/KW
[WPX] = [P] ([X]/KX) ([W]/XKW)
The binding polynomial (i.e. the sum of all the chemical forms taken by P) is:
[P]total = [P] (1 + [X]KX + [W]KW + [X]KX[W]XKW)
Although the two ligands X and W have the same thermodynamic properties and treatment, in biology we often have a "physiological" ligand, which is "more important" and a "regulatory" ligand, less important: e.g. the physiological ligand of respiratory proteins is oxygen, all others being effectors; the physiological ligand of an enzyme is its substrate, all others being inhibitors or activators; and so on. If this is the case, we may be interested in determining the fractional saturation of the protein with its physiological ligand and the effect of the regulatory ligand on it. Let us assume that the physiological ligand is X:
YX = liganded binding sites for X / total binding sites for X =
= ([X]KX + [X]KX[W]XKW) / (1 + [X]KX + [W]KW + [X]KX[W]XKW)
We remark that, as expected, if no W is present, this equation reduces to the simple mass law.
YX = [X]KX / (1 + [X]KX).
An important parameter is X50, the concentration of the physiological ligand required to achieve YX = 0.5. By equating YX to 0.5 and [X] to X50 we obtain:
X50, W = (1 + [W]KW) / KX (1 + [W]XKW)
The latter reduces to X50 = 1 / KX if either (i) no W is present ([W]=0) or (ii) the two ligands are not linked to each other (i.e. KW = XKW).
Moreover, we notice that if KX > WKX then (i) W is an inhibitor whose binding promotes the dissociation of the physiological ligand Y; (ii) KW > XKW; (iii) X50, W > X50; and (iv) the "prevalent" reaction of the system, under appropriate experimental conditions, is YP + X <==> PX + Y.
The opposite holds if KX < WKX in which case W is an activator and under appropriate experimental conditions, the "prevalent" reaction is P + X + Y <==> YPX.
1.4: ALLOSTERY IN MONOMERIC PROTEINS
Allostery is a term coined by J. Monod (Monod et al. 1963, 1965) to define a protein that is stable and binds ligands in either of two (or more) structural conformations, that for historical reasons are namend T (for tense) and R (for relaxed). The reaction scheme for the binding of a single ligand is as follows:
| KR | |||||
| RP + X | <==> | RPX | |||
| L0 | | | | | L1 | ||
| TP + X | <==> | TPX | |||
| KT |
This reaction scheme is clearly too complex to be resolved for a protein which binds a single ligand: nature can construct such a system (as it has been demonstrated by H. Frauenfelder and co-workers, see Austin et al. 1975), but we cannot determine its equilibrium constants unless it has some other reaction or property to be explored. Nevertheless it is interesting to consider this system since what we learn from its thermodynamic properties may be applied to more complex and more informative cases.
In the original formulation of the model by Monod, Wyman and Changeux (1965) the equilibrium constants were defined for the dissociation reactions; however, for the sake of consistency, I shall here use the combination reactions and the corresponding constants, defined as follows:
TKX = [TPX] / [TP][X]
RKX = [RPX] / [RP][X]
L0 = [TP] / [RP]
L1 = [TPX] / [RPX] = L0 TKX / RKX
Taking RP as the reference species we obtain:
[RPX] = [RP] RKX [X]
[TP] = [RP] L0
[TPX] = [RP] L0 TKX [X]
which leads to the binding polynomial:
Ptotal = [RP] (1 + RKX [x] + L0 + L0 TKX [X])
and to the fractional ligand saturation:
YX = [X] (RKX + L0 TKX) / (1 + L0 + RKX [x] + TKX [X])
The above equation shows that this system behaves as a simple monomeric protein with the apparent equilibrium constant:
Kapp = (RKX + L0 TKX) / (1 + L0)
In the absence of further and independent experimental evidence, we shall never be able to determine anything else than Kapp.
An interesting case is that of an allosteric monomeric protein capable of binding two ligands to two different sites; this indeed was Monod's original case of the regulatory protein of the Operon Lac in E. coli, that binds galactose and DNA. In the simplest case we assume that the R and T conformations correspond to two full thermodynamic states, whose energy is not affected by the two ligands X and W, whose only effect is to bias the allosteric equilibrium constant L:
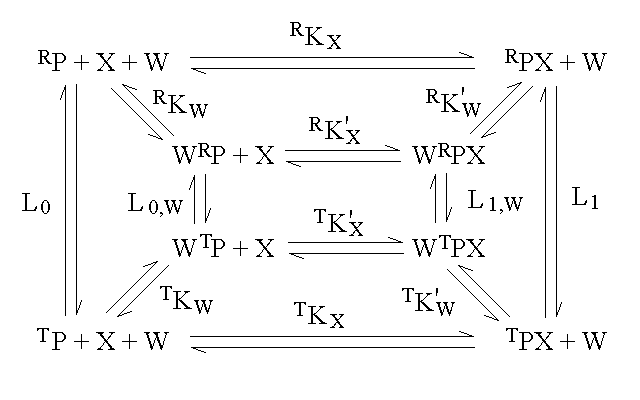
[RP] = reference concentration
[RPX] = [RP] RKX [X]
[WRP] = [RP] RKW [W]
[WRPX] = [RP] RKW [W] RK'X [X]
[TP] = [RP] L0
[TPX] = [RP] L0 TKX [X]
[WTP] = [RP] L0 TKW [W]
[WTPX] = [RP] L0 TKW [W] TK'X [X]
This scheme seems complex but, under the above assumptions, it may be simplified to a great extent: indeed if T and R are two thermodynamic states whose ligand affinity is not changed by any bound ligand, so that each K' is equal to the corresponding K, one obtains:
[RP]total = [RP] + [WRP] = [RP] (1 + RKW [W])
[TP]total = [TP] + [WTP] = [RP] L0 (1 + TKW [W])
L0, app = L0 (1 + TKW [W]) / (1 + RKW [W])
and the scheme reduces to the two state one described above, with L0, app replacing L0. We remark that if this case applies, the system is no longer underdetermined and the measurement of Kapp at different concentrations of W may in principle resolve all the five equilibrium constants.
REFERENCES
Austin R.H., Beeson K.W., Eisenstein L., Frauenfelder H. and Gunsalus I.C. (1975) Dynamics of ligand binding to myoglobin. Biochemistry 14: 5355-5373.
Monod J., Changeux J.P. and Jacob F. (1963) Allosteric proteins and cellular control systems. J Mol Biol. 6: 306-329.
Monod J., Wyman J. and Changeux J.P. (1965) On the nature of allosteric transitions: a plausible model. J Mol Biol.12: 88-118.
Go to: main page; next chapter.
Questions? write an e-mail.