Andrea Bellelli
CHAPTER 2: PRACTICAL CONSIDERATIONS
Contrary to what one might expect, this chapter will in no way be less theoretical than the preceding and the following ones. Indeed, its aim is to analyze the possible consequences of practical difficulties frequently encountered in biochemistry. I shall try to answer questions like "what will happen to my ligand binding isotherm if this or that complication occurs?". In my experience problems and complications of different types are common in biological samples, and may have disconcerting consequences; worse still they may have disconcerting but not obvious consequences that cause the scientific literature to be populated by errors. As a general rule these difficulties may be overcome by more (and more careful) experiments, more (and more critical) analysis of the experimental data, and more thinking. Repeating the same experiment with carefully planned changes in the experimental setup is an invaluable tool, but in what follows I shall consider only the most common experimental procedures and their most obvious variations.
2.1: DIRECT METHODS TO MEASURE THE CONCENTRATIONS OF BOUND AND FREE LIGAND
In order to determine the equilibrium constant and stoichiometry of the combination reaction of a protein with its ligand, one should measure the concentrations of three chemical species, that in the preceding chapter we indicated as P, L and PL. Direct methods are the most straightforward, and aim exactly to the objective; an incomplete list includes: (i) chemical determination by quantitative analysis (may require the equilibrium dialysis method); (ii) potentiometric methods (usually only for the ligand, if it is suitable for a redox reaction: e.g. oxygen, NO); (iii) radiometric methods (a radioactive ligand should be used); (iv) spectrophotometric methods (absorbance and CD spectroscopy are directly proportional to concentration, and fluorescence is also with some limitations, and only on a comparative scale); (v) gravimetric methods; (vi) gas manometric or gas volumetric methods (these were classically employed for gaseous ligands: e.g. the oxygen content of human blood was estimated at 21% v/v).
The application of direct methods requires that the system has reached its equilibrium condition before any measurement is made, and that the analysis does not perturb this condition. The second requirement may be hard to meet (e.g. if a destructive method is used to determine the concentration of the free ligand, this promotes the dissociation of the bound ligand and the total ligand is measured instead of the free ligand). Moreover, not all ligands and proteins lend themselves to the use of direct methods. I shall describe in what follows some typical examples.
Measurement of the oxygen binding isotherms of myoglobin using the method of Rossi-Fanelli and Antonini (Arch. Biochem. Biophys. 1958, 77, 478-492): the chemical reaction is Mb + O2 <==> MbO2. The equilibrium condition is reached very rapidly but in this method the reaction is eterogenous, the ligand being added in the gas phase: thus one should wait under delicate agitation until the gaseous and water phases are fully equilibrated at the desired temperature (time depends on the volume of the liquid phase; for small volumes 5-10 min. are usually sufficient). The preparation of the experiment is as follows: 1-2 ml of a solution of the protein in the desired buffer is poured into a tonometer sealed to a glass spectrophotometric cuvette. Given that the extinction coefficient of Mb in the visible region of the spectrum (650-500 nm) is approx. 15 /mM.cm, the concentration required if one uses an optical path of 2 mm is approx. 0.3 mM (or 4.5 mg/mL).
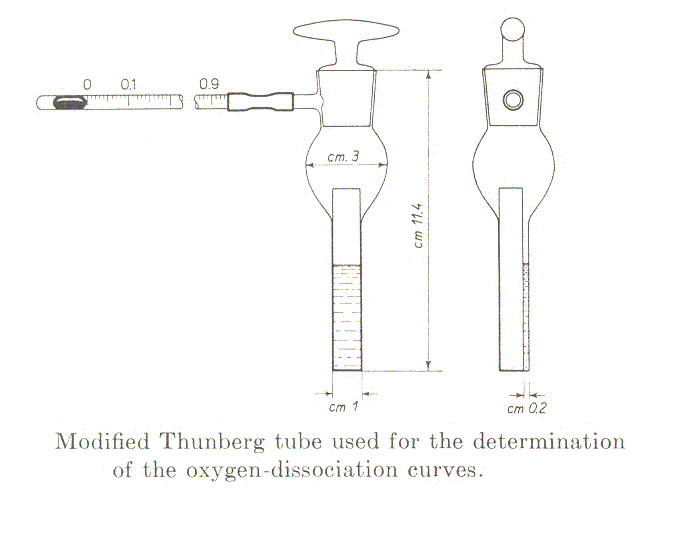
The tonometer is gently evacuated using a vacuum pump, taking care of maximixing the area of the liquid-gas interface and the absorbance spectrum is recorded. The procedure is repeated until the characteristic absorbance spectrum of deoxygenated Mb is obtained. The spectrum is saved and air is added by connecting the tonometer to a 1 mL graduated glass pipette containing one drop of mercury. The volume of air added is annotated and the solution is allowed to equilibrate with the gas phase for 5 min. under agitation in a water bath at the desired temperature; then a new spectrum is recorded. The entire procedure is repeated several times, till the absorbance spectrum corresponds to that of oxyMb. At the end of the experiment the abosrbance spectra recorded will be similar to those depicted below:
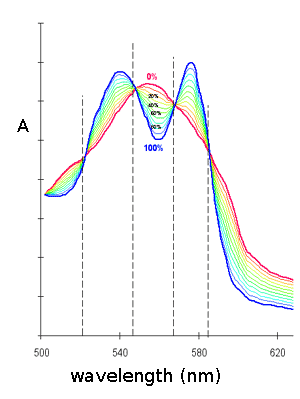
The fractional saturation of Mb is:
Y = [MbO2] / ([Mb]+[MbO2])
and can be calculated taking advantage of the absorbance readings at wavelengths selected for the greatest differences between Mb and MbO2 (i.e. at peaks of the difference spectrum). If one uses a single wavelength, the formula is as follows:
Y = (Ai - AMb) / (AMbO2 - AMb)
However it is safer to mediate the Y values of each spectrum as calculated from at least two or three wavelength, possibily taken at positive and negative peaks of the difference spectrum (e.g. at 576, 555 and 540 nm). Good isosbestic points guarantee that the reaction mechanism is simple (i.e. that only two chromophores are present, Mb and MbO2, and that the sum [Mb]+[MbO2] is constant, as expected), and that no significant baseline drifts occurred during the experiment.
The partial pressure of oxygen inside the tonometer is calculated volumetrically, from the dilution factor, i.e.:
PO2 = PO2 air * vol.O2 added / vol.tonometer
To estimate the internal volume of the tonometer one should weight the empty and water filled tonometer on a precision balance; obviously the volumes of the Mb solution and of the spacer (if used) should be subtracted. The PO2 thus calculated neglects the amount of oxygen present in the aqueous phase, either dissolved in solution or bound to Mb. This is usually acceptable, since only a very minor fraction of the total gas is present in the aqueous phase.
The final product of the experiment is a graph of Y vs. PO2, or, more often, a family of such graphs recorded at different pH, temperature or other variable of interest:
Measurement of the oxygen binding isotherms of myoglobin using the method of K. Imai. Kihoiro Imai developed an instrument capable of automatically recording the oxygen binding isotherms of myoglobin and hemoglobin.
2.2: INDIRECT METHODS: REPLACEMENT OF, AND LINKAGE WITH, OTHER LIGANDS
Indirect methods are resorted to when the application of direct methods is impractical: this may occur because of several reasons, the most important and most frequently encountered of which are: (i) poor signal; or (ii) very high affinity. Poor signal is due to the species P being difficult to distinguish from PL and the species L being difficult to distinguish from PL; a possible example is the case of fatty acids binding to the Fatty Acid Binding Protein (FABP; see below). A typical case of poor signal is that of enzyme inhibitors: indeed it is quite uncommon for enzyme inhibitors to be chromogenic so that their combination with the target enzyme can be detected spectroscopically (as it occurs in the case of Cibachron blue binding to lactate dehydrogenase); given that the enzyme activity is influenced and is very easy to measure, almost all the affinities of enzyme inhibitors have been determined using indirect (linkage) methods. Very high affinity of the ligand for the protein causes the free ligand concentration required to measure the equilibrium constant to be accordingly low, which means not only difficult to determine, but also technically demanding because of the requirement to reduce the protein concentration to undetectable levels. This problem can be overcome by replacement methods, as it has been often done in the case of the measurement of the affinity of hemoglobin and myoglobin for CO by replacement of bound oxygen (see below).
Measurement of fatty acid binding to Fatty Acid Binding Protein. This reaction conforms to the general scheme P + L <==> PL but neither the protein nor the ligand yield absorbance or fluorescence changes upon binding (radioactive or fluorescent analogues of of the ligand can be employed, if available), but competition between the fatty acid and the fluorophore Anilino Naphtalene Sulfonate is observed
2.3: HIGH AFFINITY LIGANDS
In many cases the measurement of an equilibrium constant for a protein-ligand couple is measured on a sample of the chosen protein successively equilibrated with increasing concentrations of the ligand. The liganded and unliganded protein must differ by some kind of measurable property, and this sould provide a "signal" recorded by a suitable instrument. A straightforward example is given by proteins whose spectroscopic (e.g. absorbance or fluorescence) properties change as a consequence of ligation: in this case the signal is a difference in the extinction coefficient or quantum yield of P and PX. Tipically, the researcher prepares a spectrophotometric cuvette containing the appropriate volume of a solution of the protein with suitable signal, and adds successive aliquots of a concentrated solution of the ligand. Ideally an interval of free ligand concentrations spanning at least two logaritmic units and centered on -log K should be explored, with some 5-10 points equally spaced on the logarithm of ligand concentration.
The experiment described above is by no means unique or special: many other signals and experimental setups can be employed: e.g. if radioactive, or otherwise labelled, ligand is available a dialysis equilibrium can be resorted to.
A fundamental point to be taken into account is the ratio between the minimal protein concentration required to provide a readable signal and the equilibrium constant. We can consider two cases, i.e. (i) [P]total K << 1 and its opposite (ii) [P]total K >> 1. Classical examples are the equilibria of myoglobin with O2, with K in the 106 M-1 range, and with CO, with K in the 108 range. Given that the extinction coefficients of Mb are, at most, in the 105 range, it is obvious that case (i) is at most approximated for O2, whereas case (ii) is fulfilled for CO.
Given that the total ligand added to the system will be partitioned between the free ligand in solution (X), whose concentration appears in the mass law, and the bound ligand (PX), if we are in the conditions described by case (i) then the relation [PX] << [X] will apply allover the experiment. This is usually an advantageous condition if we aim at measuring K, since [PX] is measured by the signal and [X] is close to [X]total, thus minimizing the errors in its determination. Figure 2.1.1 reports a simulation of this condition, calculated with the following parameters K = 104 M-1, [P]total = 10-6 M, [X]total ranging from 10-5 M to 10-3 M (o). [X] is calculated by subtracting Y [P]total from [X]total (*), but this correction is unnecessary, and we can safely approximate [X] to [X]total.
If the signal provided by our protein is small or K is large, our experiment will require [P]total > 1 / K and we will be in case (ii). This condition is unfavorable to a precise determination of K since it entails [PX] >> [X] and [X]total will approximate [PX], whereas [X] will be small. Thus we should expect significant errors in the estimate of [X], and consequently of K (we should remember that 1/K is a point on the X axis). In the limiting case in which [X] is negligible with respect to [X]total, the plot of Y vs. [X]total yields a straight line and is called a titration. A titration is useless for the measurement of K, but yields a very relevant information, since it allows one to estimate the concentration of the binding sites for X, and hence the stoichiometry P:X (that in the present chapter is assumed as unitary).
How can we measure very high Ks? The most straightforward answer to this question would be to dilute the protein to less than 1/K, but this solution is not always practical: we are limited by the concentration of P required to provide a reliable signal. Another solution is to find a lower affinity competitive ligand W, to measure its affinity KW, and then to record the replacement of W by X and the relative partition constant: as demonstrated in chapter 1.2, the partition constant equals the ratio of the affinity constants of the two ligands, and KX = Kp KW: a value too great to be determined experimentally has been decomposed into the product of two much smaller values. Other types of competitions may be resorted to if a competitive alternative ligand is not available: indeed we may exploit the partition of the ligand X between two phases, only one of which contains the protein (e.g. the gas phase for O2 or CO, or an organic immiscible solvent for a ligand that has greater solubility in this solvent than in water; the free ligand is then measured in the phase in which the protein is absent and the bound ligand in that where the protein is present). Finally, we may consider the possibility of lowering the affinity of the protein by changing the experimental conditions: temperature, pH and buffer composition.
2.4: THERMODYNAMIC REVERSIBILITY
Equilibrium considerations as those discussed in chapter 1 are meaningful only for reversible chemical reactions that have reached their equilibrium condition before any concentration is measured. Irreversible reactions, especially slow irreversible reactions may often be misinterpreted as reversible; obviously no equilibrium constant can be calculated for an irreversible reaction and any attempt to do so is domed to failure, often to an unrecognized failure. In theory irreversible reactions do not exist and the whole subject matter should be treated under the subheading of high affinity ligands: indeed a truly irreversible ligand that completely binds to the protein and leaves a zero concentration in solution (provided that the protein is in excess) would have an infinite affinity constant and consequently an infinitely negative ΔG0, resulting from the relation ΔG0 = -RT ln K. This is forbidden by the first principle of thermodynamics. Even though "irreversible" merely stands for "very high affinity", in practice there is a border between ligands whose affinity is in the order of, say, K=1010 M-1 and ligands whose affinity is in the order of, say, K=1020 M-1: in the former case the free ligand concentration in solution is low and difficult to measure; in the latter case the protein equilibrates with a few molecules of free ligand or even with less than one (i.e. one molecule of free ligand is present at some times and absent at other times), and thus the free ligand concentration escapes detection. Binding constants in excess of 1020 M-1 are not uncommon in biochemistry, an obvious example being the coordination of metals to the sulfur atom of Cys residues.
In order to be confident on the measurements he is carrying out, the scientist is strongly advised to carry out control measurements, i.e.: (i) to demonstrate reversibility of the binding by removing the bound ligand (usually by dialysis); and (ii) to record the equilibrium curve of his/her chosen protein-ligand couple both in the direction of the combination and in that of dissociation.
Ligand removal by dialysis is straighforward: the protein ligand complex is dialyzed against a suitable buffer with repeated exchanges of the dialysis buffer, then the protein solution is checked for the presence of any residual ligand with the usual means. It is important to stress that dialysis is expected to remove both the protein-bound and the free ligand and thus the dialyzed solution must be free of ligand and must contain unliganded protein. The unliganded protein thus obtained must be able to bind ligand again if it is added. Other methods to remove the ligand, that are expected to convert the protein-ligand complex into the fully functional unliganded protein are the chemical destruction of the ligand in solution (e.g. O2 bound to hemoglobin is destroyed by dithionite) or competition with a second protein capable of binding the same ligand.
Carrying out a ligand binding experiment in the two directions of combination and dissociation is more complex and not always possible. A straighforward example is provided by the equilibrium of oxygen with hemoglobin (Hb) or myoglobin (Mb) using the instrument developed by K. Imai. The instrument is a gas tight chamber which contains a solution of Hb or Mb equilibrated with a gas phase of known composition; the oxygen saturation of the protein is measured spectroscopically, taking advantage of two glass windows. An oxygen combination experiment is carried out by equilibrating the chamber with nitrogen (this yields deoxyHb or deoxyMb as a starting material) and then replacing the gas with a mixture of oxygen and nitrogen; an oxygen dissociation experiment is carried out by equilibrating the chamber with oxygen and washing with nitrogen. Imai was able to demonstrate that the equilibrium curves of oxygenation and deoxygenation thus recorded are perfectly superimposable (see Imai, 1981).
2.5: KINETIC PROBLEMS: WHAT IF EQUILIBRATION IS SLOW
2.6: LOW AFFINITY LIGANDS
2.7: MIXTURES OF ISOFORMS
REFERENCES
Imai K. (1981) Measurement of accurate oxygen equilibrium curves by an automatic oxygenation apparatus. Methods Enzymol. 76: 438-449.
Go to: main page; next chapter.
Questions? write an e-mail.